Свойства сходящихся рядов

Теорема 1. Если в ряде отбросить конечное число первых членов, то полученный ряд и ряд сходятся или расходятся одновременно.

Теорема 2. Если ряды и 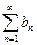сходятся и С – некоторое число, то ряды 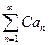и 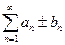также сходятся, при этом , .

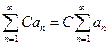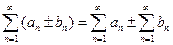Теорема 3. (необходимый признак сходимости ряда). Если ряд сходится, то .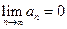

Следствие (достаточное условие расходимости ряда). Ес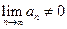ли или 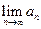не существует, то ряд расходится.

Замечание. Условие 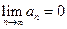является необходимым, но не достаточным для сходимости, т.е. если 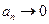, то ряд может сходиться, а может и расходиться.

Пример.Исследовать сходимость ряда .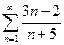

Решение. Ряд 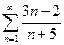расходится, т.к. 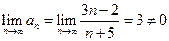, т.е. выполняется достаточное условие расходимости ряда.

Пример.Исследовать сходимость ряда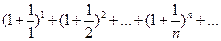

Решение.Данный ряд расходится, т.к. .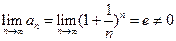

Пример.Исследовать сходимость ряда .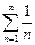

Решение. 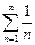= 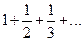, для него 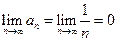, но этот ряд является расходящимся. Докажем это. Предположим, что ряд сходится и его сумма равна S, тогда имеем 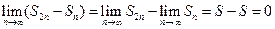. С другой стороны,

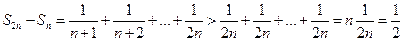. Значит, 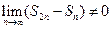. Полученное противоречие, доказывает, что данный ряд не может сходиться. Данный ряд называется гармоническим.

Теорема 4 (Критерий Коши). Для того, чтобы ряд сходился, необходимо и достаточно, чтобы для 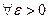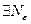такой, что при 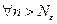неравенство 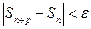выполнялось для любого конечного .

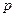Т. е. сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.