Достаточные признаки сходимости положительных рядов
Определение.Вещественный ряд  называют положительным, если
называют положительным, если 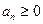 для
для 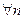 .
.
Пусть даны два положительных ряда  и
и 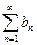 .
.
Теорема 5 (Признак сравнения).Пусть, начиная с некоторого номера, 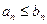 . Тогда:
. Тогда:
· из сходимости ряда 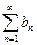 следует сходимость ряда
следует сходимость ряда  ;
;
· из расходимости ряда  следует расходимость ряда
следует расходимость ряда 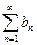 .
.
Теорема 6 (Предельный признак сравнения). Пусть существует предел 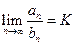
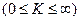 . Тогда:
. Тогда:
· при 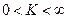 ряды
ряды  и
и 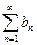 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;
· при 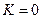 из сходимости ряда
из сходимости ряда 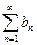 следует сходимость ряда
следует сходимость ряда  .
.
· при 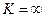 из расходимости ряда
из расходимости ряда 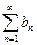 следует расходимость ряда
следует расходимость ряда  .
.
Пример.Исследовать на сходимость ряд 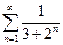 .
.
Решение. Сравним данный ряд с рядом геометрической прогрессии 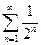 , который сходится (
, который сходится ( 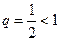 ). Имеем
). Имеем 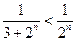 . Следовательно, по теореме 5 данный ряд сходится.
. Следовательно, по теореме 5 данный ряд сходится.
Пример.Исследовать на сходимость ряд 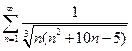 .
.
Решение. Рассмотрим ряд 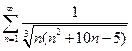 . Сравним этот ряд с гармоническим рядом:
. Сравним этот ряд с гармоническим рядом: 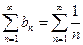 , который расходится. Так как
, который расходится. Так как 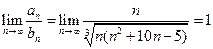 , то по теореме 6 исходный ряд расходится.
, то по теореме 6 исходный ряд расходится.
Пример. Исследовать на сходимость ряд 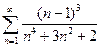 .
.
Решение. Исследуем сходимость этого ряда с помощью предельного признака сравнения. Так как 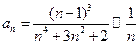 при
при 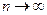 , (эти величины эквивалентны), то для сравнения берем ряд с общим членом
, (эти величины эквивалентны), то для сравнения берем ряд с общим членом 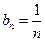 , т.е. ряд
, т.е. ряд 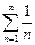 (гармонический ряд). Имеем:
(гармонический ряд). Имеем: 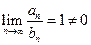 . Следовательно, по предельному признаку сравнения исходный ряд расходится.
. Следовательно, по предельному признаку сравнения исходный ряд расходится.
Замечание.Применяя признаки сравнения, рекомендуется использовать ряды, сходимость которых заранее известна. Такими рядами, в частности, являются: ряд геометрической прогрессии, гармонический ряд и обобщенный гармонический ряд, сходимость которого будет исследована позже.
Теорема 7 (Признак Даламбера). Пусть  - положительный ряд, и существует конечный или бесконечный предел
- положительный ряд, и существует конечный или бесконечный предел 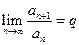 (
( 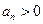 ). Тогда, при
). Тогда, при 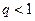 ряд
ряд  сходится, а при
сходится, а при 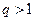 - расходится.
- расходится.
Пример.Исследовать на сходимость ряд 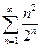 .
.
Решение. Обозначим 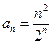 ,
, 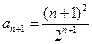 . Применяя признак Даламбера, получаем
. Применяя признак Даламбера, получаем 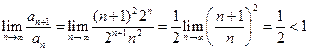 . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Пример.Исследовать на сходимость ряд 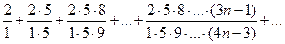 ;
;
Решение. 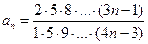 ,
, 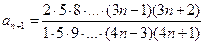 . Тогда
. Тогда 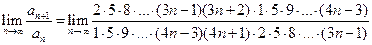 =
= 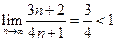 . Ряд сходится.
. Ряд сходится.
Теорема 8 (Радикальный признак Коши).Пусть  - положительный ряд и существует конечный или бесконечный предел
- положительный ряд и существует конечный или бесконечный предел 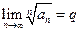 . Тогда, при
. Тогда, при 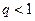 ряд
ряд  сходится, а при
сходится, а при 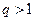 - расходится.
- расходится.
Пример.Исследовать на сходимость ряд 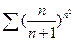 .
.
Решение. Применяя признак Коши, получим 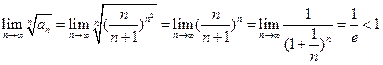 . Ряд сходится.
. Ряд сходится.
Пример.Исследовать на сходимость ряд 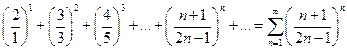 .
.
Решение. Применяя признак Коши для исследования сходимости ряда: 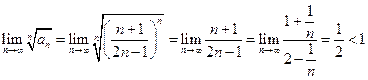 , поэтому ряд сходится.
, поэтому ряд сходится.
Замечание. Применяя признак Коши, полезно использовать пределы 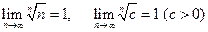 и формулу Стирлинга
и формулу Стирлинга 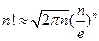 , выражающую значение
, выражающую значение 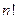 через степенную функцию. Здесь знак
через степенную функцию. Здесь знак 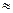 означает, что указанные бесконечно большие величины эквивалентны.
означает, что указанные бесконечно большие величины эквивалентны.
Замечание. При 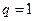 признаки Даламбера и Коши не дают ответ на вопрос о сходимости ряда. В этом случае необходимы дополнительные исследования. Иногда здесь помогают более сложные признаки (признаки Раабе, Гаусса и другие). Во многих случаях эффективен интегральный признак Коши.
признаки Даламбера и Коши не дают ответ на вопрос о сходимости ряда. В этом случае необходимы дополнительные исследования. Иногда здесь помогают более сложные признаки (признаки Раабе, Гаусса и другие). Во многих случаях эффективен интегральный признак Коши.
Пусть числовой ряд имеет вид 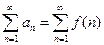 , т.е. каждый член ряда может быть записан как значение некоторой функции
, т.е. каждый член ряда может быть записан как значение некоторой функции 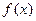 при целочисленных значениях аргумента. Причем функция
при целочисленных значениях аргумента. Причем функция 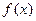 непрерывна, положительна и монотонно убывает. Функция
непрерывна, положительна и монотонно убывает. Функция 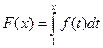 будет монотонно возрастающей, т.к.
будет монотонно возрастающей, т.к. 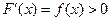 , т.е. при
, т.е. при 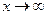
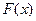 будет иметь конечный либо бесконечный предел, а следовательно, и несобственный интеграл
будет иметь конечный либо бесконечный предел, а следовательно, и несобственный интеграл 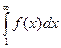 будет либо сходящимся, либо расходящимся.
будет либо сходящимся, либо расходящимся.
Теорема 9 (Интегральный признак Коши).Ряд  и несобственный интеграл
и несобственный интеграл 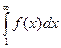 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример. Исследовать на сходимость обобщенный гармонический ряд (ряд Дирихле): 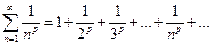 , где
, где 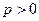 - действительное число,
- действительное число,
Решение. Для исследования сходимости применим интегральный признак Коши (признаки Даламбера и Коши ответа о сходимости не дают). Рассмотрим функцию 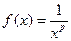 . Эта функция непрерывна, монотонно убывает на промежутке
. Эта функция непрерывна, монотонно убывает на промежутке 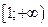 и
и 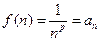 . При
. При 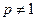 имеем:
имеем: 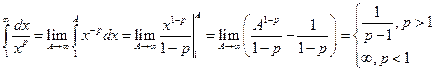 .
.
При 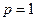 имеем гармонический ряд
имеем гармонический ряд 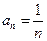 , который расходится (
, который расходится ( 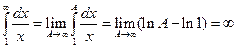 ).
).
Таким образом, обобщенный гармонический ряд сходится при 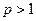 , расходится при
, расходится при 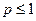 .
.
Дата добавления: 2016-01-09; просмотров: 1105;
