Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.

При изучении в рядах динамики основной тенденции развития явления применяются следующие приемы и методы. Одним из приемов, относящихся к самым простым методов выявления основной тенденции является метод укрупнения интервалов, который позволяет в значительной степени абстрагироваться от случайных колебаний. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.

При этом используют либо переменную среднюю, либо скользящую среднюю. Исчисление итогов за укрупненный период возможно, только по интервальным pядам, расчет средней по укрупненным интервалам осуществляется по формуле средней арифметической простой.

Например, укрупненный интервал образован объединением трех периодов, средние для укрупненных интервалов определяются следующим образом:

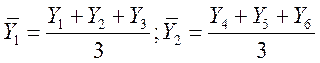и т.д.

где У₁, У₂, У₃, …, Y₅ — уровни исходного ряда динамики.

2. МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ ПРИ ВЫЯВЛЕНИИ ТРЕНДА

. Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.

Средняя исчисляется также по среднёй арифметической простой, но не за изолированные укрупненные периоды, а со сдвигом на один период. Если в динамическом ряду имеются периодические колебания, то период средней скользящей должен совпадать с периодом колебания или быть кратным ему. Если в ряду отсутствуют периодические колебания, то укрупненный период целесообразно выбрать равным трем, так в этом случае рассчитанная средняя будет записана в середине трехлетнего периода, т.е. приписана к конкретному периоду. Скользящие средние с продолжительностью периода, равной 3, будут следующие:

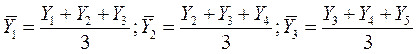и т.д.

Если период скользящей средней четный, то выполняют центрирование данных, т.е. определение средней из найденных средних, что необходимо для определения среднего периода. Например, если исчисляется скользящая средняя с продолжительностью периода равной 2, то расчет производится следующим образом:

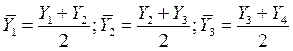и т.д.

Тогда центрированные средние равны:

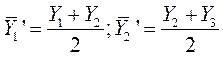и т.д.

Рассмотренные методы позволяют выявить тенденцию развития, но не могут быть использованы для прогнозирования. Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. Под аналитическим выравниванием понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени.

Его сущность заключается в том, что находится уравнение, выражающее закономерность изменения явления как функции времени .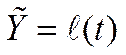

Вид уравнения определяется характером динамики развития явления. Как уже было ранее отмечено:

•если абсолютные приросты стабильны, та аналитическое выравнивание может быть выполнено по прямой;

• если абсолютные приросты равномерно увеличиваются, то можно сглаживание производить по параболе второго порядка;

• если стабильны темпы роста, то целесообразно использовать показательную функцию.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f­(t) . На практике по имеющемуся временному ряду задают вид и находят параметры функции ­ f­(t), а затем анализируют поведение отклонений от тенденции. Функцию ­ f­(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления, на основе графического изображения уровней динамического ряда.

Выбор формы кривой может быть определен. Наиболее часто используются функции:

• линейная ;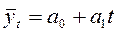

• парабола второго порядка ;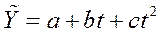

• показательная ;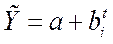

• гиперболическая ;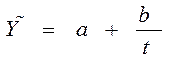

· экспоненциальные ­ f­(t) = ехр (а₀ + а­₁t )

· или ­ f­(t) = ехр(а₀ + а­₁t+ а­₂t²­)

В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели

У_t = f­(t) + e_t.

где f­(t) - уровень, определяемый тенденцией развития;

e_t - случайное и циклическое отклонение от тенденции.

Оценка параметров (а₀,а­₁,а­₂­,....)осуществляется следующими методами:

1) методом избранных точек,

2) методом наименьших расстояний,

3) методом наименьших квадратов (МНК).

В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:

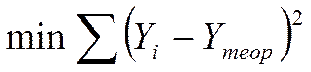
Для линейной зависимости f­(t) = а₀ + а­₁t параметр а₀, обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а₁ - сила связи, т. е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а­ можно представить как постоянный теоретический абсолютный прирост.

Расчеты значительно упрощаются, если начало отсчета времени поместить в середину динамического ряда, тогда сумма временных дат будет равна нулю Σt = 0, и система нормальных уровней значительно упрощается и преобразуется в следующий вид:

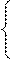
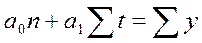
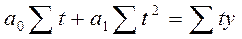
Решение системы уравнений позволяет получить выражения для параметров 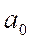и :

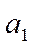откуда: 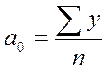представляет собой средний уровень ряда динамики ( );

.

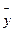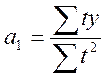Аналитическое выравнивание позволяет не только определить основную тенденцию изменения явления на исследуемом отрезке времени, но выполнять расчеты для таких периодов, для которых нет информации. Нахождение недостающих данных внутри динамического ряда называется интерполяцией, а нахождение значений за пределами анализируемого периода называется экстраполяцией.