Прогнозирование на основе экстраполяции предполагает, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда.
При составлении прогнозов социально-экономических явлений обычно оперируют интервальной оценкой, т.е. рассчитывают так называемые доверительные интервалы прогноза с заданной вероятностью.
Границы интервалов определяются по формуле:
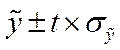 ,
,
где 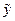 - точечный прогноз, рассчитанный по модели;
- точечный прогноз, рассчитанный по модели;  - ошибка прогноза (среднее квадратическое отклонение фактических уровней от расчетных по модели); t – коэффициент доверия по распределению Стъюдента.
- ошибка прогноза (среднее квадратическое отклонение фактических уровней от расчетных по модели); t – коэффициент доверия по распределению Стъюдента.
Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт) сравнивается с теоретическим (табличным) значением:

Где k - число параметров функции, описывающей тенденцию; n - число уровней ряда;
Fфакт сравнивается с Fтеор (по таблицам) при v1 = (k - 1 ), v2 = (n - k) степенях свободы и уровне значимости a (обычно a = 0,05). Если Fфакт > Fтеор, то уравнение регрессии значимо, т. е. построенная модель адекватна фактической временной тенденции.
Для аппроксимации процесса изменения во времени используют несколько моделей, а наилучшую пригодность проверяют на основе принципа минимизации квадратов отклонений фактических и выравненных (теоретических) значений динамического ряда.
Дата добавления: 2016-02-04; просмотров: 936;
