Параболический тренд и его свойства
Под названием параболического будем иметь в виду тренд, выраженный параболой II порядка с уравнением
 .
.
Параболы III порядка и более высоких порядков редко применимы для выражения тенденции динамики и слишком сложны для получения надежных оценок параметров при ограниченной длине временного ряда. Прямую линию, с точки зрения математики, можно также считать одним из видов парабол - параболой I порядка, которая уже рассмотрена ранее.
Значения (смысл, сущность) параметров параболы II порядка таковы: свободный член а— это средний (выравненный) уровень тренда на момент или период, принятый за начало отсчёта времени, т.е. t=0; b— это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется рaвномерно со средним ускорением, равным 2 с, которое и служит константой, главным параметром параболы II порядка.
Основные свойства тренда в форме параболы II порядка таковы:
1) неравные, но равномерно возрастающие или равномерно убывающие абсолютные изменения за равные промежутки времени;
2) парабола, рассматриваемая относительно ее математической формы, имеет две ветви: восходящую с увеличением уровней признака и нисходящую с их уменьшением. Но относительно статистики по содержанию изучаемого процесса изменений трендом, выражающим определенную тенденцию развития, чаще всего можно считать только одну из ветвей:
Либо восходящую, либо нисходящую. В особых, более конкретных ситуациях мы не отрицаем возможности объединения обеих ветвей в единый тренд;
3) так как свободный член уравнения а как значение показателя в начальный момент (период) отсчета времени, как правило, величина положительная, то характер тренда определяется знаками параметров b и с:
а) при b>0 и с>0 имеем восходящую ветвь, т.е. тенденцию к ускоренному росту уровней;
б) при b<0 и с<0 имеем нисходящую ветвь — тенденцию к ускоренному сокращению уровней;
в) при b>0 и с<0 имеем либо восходящую ветвь с замедляющимся ростом уровней, либо обе ветви параболы, восходящую и нисходящую, если их по существу можно считать единым процессом
г) при b<0 и с>0 имеем либо нисходящую ветвь с замедляющимся сокращением уровней, либо обе ветви — нисходящую и восходящую, если их можно считать единой тенденцией;
4) при параболической форме тренда, в зависимости от соотношений между его параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время возрастать, но при достаточно длительном периоде рано или поздно темпы роста обязательно начинают уменьшаться, а темпы сокращений уровней при b <0 и с<0 обязательно начинаrот возрастать (по абсолютной величине относительного изменения).
Параметры параболического уравнения определяются из системы уравнения:
для параболы 

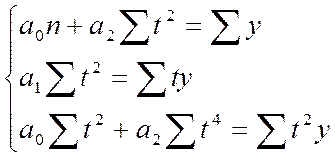
Дата добавления: 2016-02-04; просмотров: 1400;
