Вторая группа показателей, характеризующих силу сезонных колебаний, включает следующие.
1. Размах колебаний – разность между максимумом и минимумом месячных уровней:
R = Ymax-Ymin.
2. Относительный размах – отношение абсолютного размаха либо к среднему уровню, либо к максимуму, либо к минимуму:
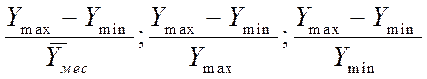 .
.
3. Среднее абсолютное отклонение месячных уровней от среднемесячного:
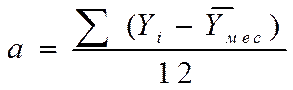 .
.
4. Относительное отклонение (ρ) – отношение среднего абсолютного отклонения к среднемесячному уровню:
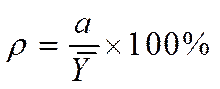 .
.
5. Среднее квадратическое отклонение месячных уровней от среднемесячного или выравненных значений за соответствующие месяцы:
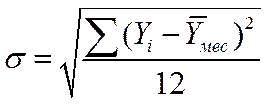 .
.
6. Коэффициент сезонных колебаний:
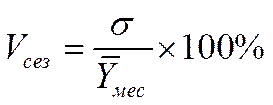 .
.
Как среднеквадратическое отклонение, так и коэффициент сезонных колебаний – это наиболее точные показатели измерения силы сезонных колебаний.
7. Обобщающий показатель сезонных колебаний, исчисленный на основе индивидуальных индексов сезонных колебаний как средняя арифметическая величина:
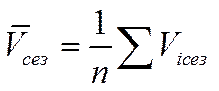 ,
,
где 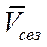 - обобщающий показатель сезонных колебаний;
- обобщающий показатель сезонных колебаний; 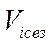 - индексы сезонных колебаний за отдельные периоды; n – число периодов.
- индексы сезонных колебаний за отдельные периоды; n – число периодов.
В статистике принято считать, что если коэффициент сезонных колебаний меньше 10 % - сезонные колебания слабые, от 10 до 25 – умеренные; от 25 до 40 – сильные и свыше 40% - очень сильные.
Если сезонные колебания изучаются за несколько лет, то целесообразно отделить их от изменений уровней за счет тенденции и от случайных колебаний, искажающих характер сезонной волны в отдельные годы.
В таком случае применяется следующая методика, изложенная в учебнике «Общая теория статистики» И.И. Елисеевой, М.М. Юзбашева.
1. По месячным или квартальным уровням за ряд лет вычисляется тренд и выравненные значения ( 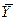 ).
).
2. Рассчитываются индексы сезонных колебаний:
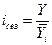 .
.
3. Эти индексы сезонных колебаний усредняются за все годы как средневзвешенные величины.
4. Уровни тренда умножаются на эти средние индексы сезонных колебаний, и получаются уровни тренда с учетом сезонной волны ( 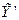 ).
).
Общую сумму квадратов отклонений фактических уровней динамического ряда от среднего уровня за все годы можно разложить на составляющие элементы:
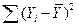 - общая сумма квадратов;
- общая сумма квадратов;
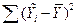 - общая сумма квадратов за счет тренда;
- общая сумма квадратов за счет тренда;
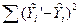 - за счет сезонности;
- за счет сезонности;
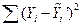 - за счет случайных колебаний.
- за счет случайных колебаний.
Дата добавления: 2016-02-04; просмотров: 1619;
