Ряды Тейлора и Маклорена

Прежде чем говорить о рядах Тейлора выведем формулу Тейлора.

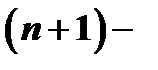Предположим, что функция имеет все производные до го порядка включительно в некотором промежутке, содержащем точку 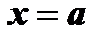. Найдем многочлен 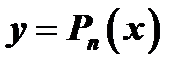степени не выше 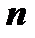, значение которого в точке 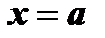равняется значению функции 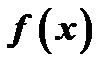в этой точке, а значения его производных до 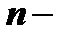го порядка в точке 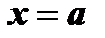равняются значениям соответствующих производных от функции 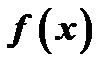в этой точке

. (13)

Естественно ожидать, что такой многочлен в некотором смысле «близок» к функции .

Будем искать этот многочлен в форме многочлена по степеням 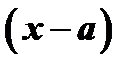с неопределенными коэффициентами

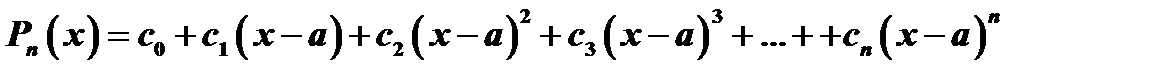. (14)

Коэффициенты 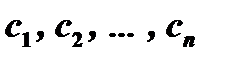определим так, чтобы удовлетворялись условия (13). Предварительно найдем производные от

(15)

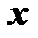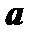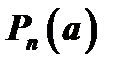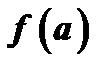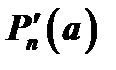Подставляя в левые и правые части равенства (14) и (15) вместо значение и заменяя на основании равенства (13) через , через 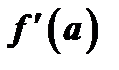и т.д., получим:

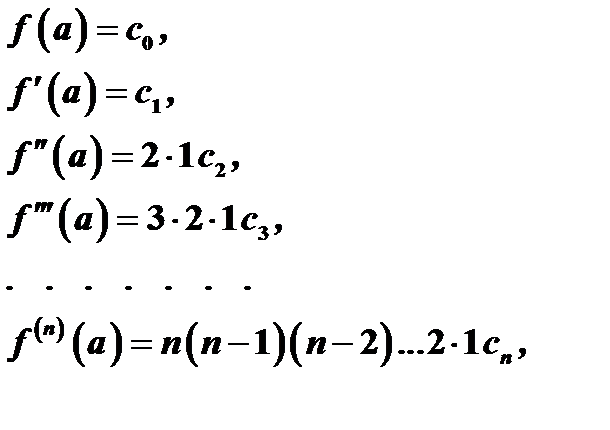
откуда находим

(16)

Подставляя найденные значения 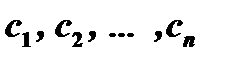в формулу (14), получим

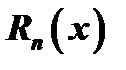. (17) Обозначим через разность значений данной функции 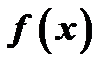и построенного многочлена 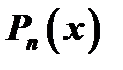: 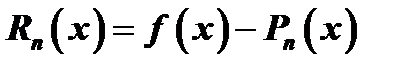, откуда 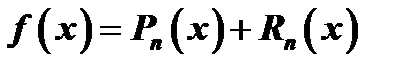, или в развернутом виде

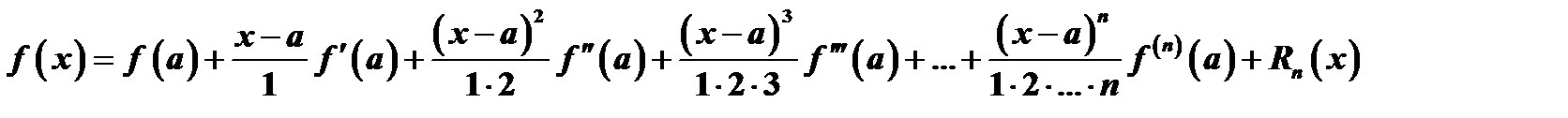
Последнее выражение называется формулой Тейлора.

Допустим, что в рассматриваемой окрестности точки 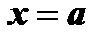, тогда, переходя к пределу, справа получим бесконечный ряд, который называется рядом Тейлора: (18)

Если в ряде Тейлора положим 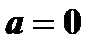, то получим частный случай ряда Тейлора, который называется рядом Маклорена:

(19)

На примере покажем разложение функции 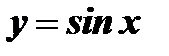в ряд Маклорена.

Подставив полученные значения в формулу (19), получим:

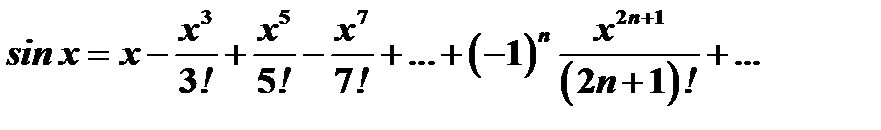
Поступая аналогичным образом, получим разложение в ряд Маклорена функций:

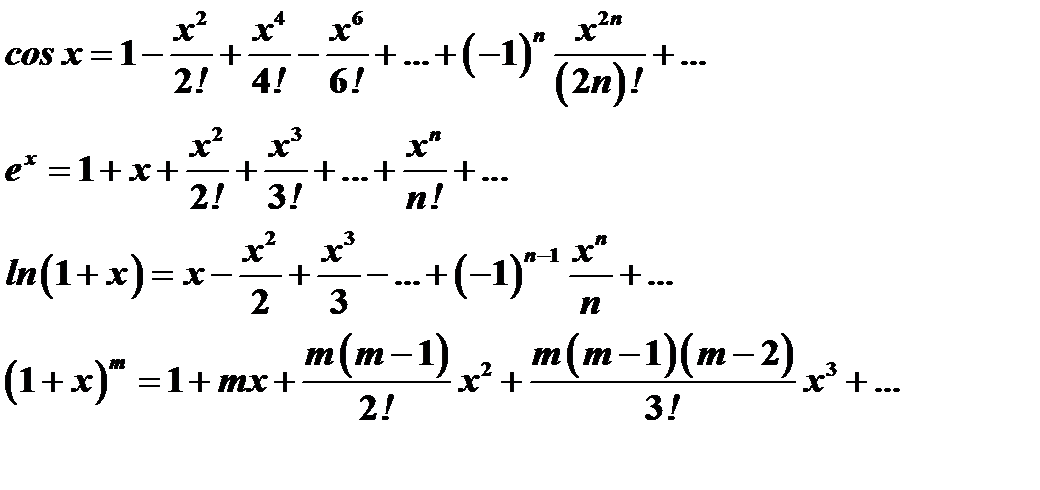
Ряды Фурье

Функциональный ряд вида

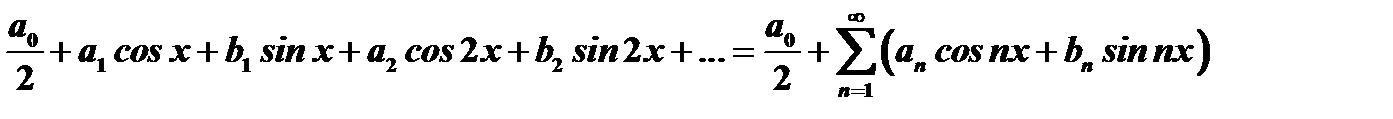(20)

называется тригонометрическим рядом, где 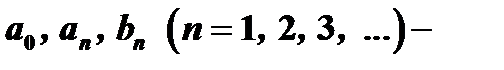коэффициенты тригонометрического ряда. Если ряд (20) сходится, то его сумма есть периодическая функция 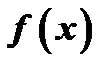с периодом 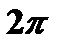, так как и являются периодическими функциями с периодом 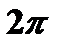. Таким образом 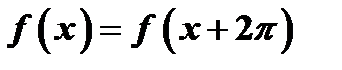. Определим коэффициенты ряда (20).

Пусть периодическая с 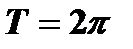функция такова, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале 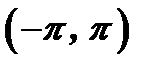, т.е. является суммой этого ряда:

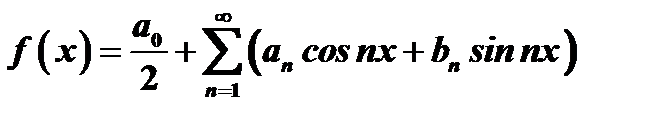. (21)

Проинтегрируем обе части равенства (21) в пределах от 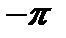до :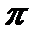

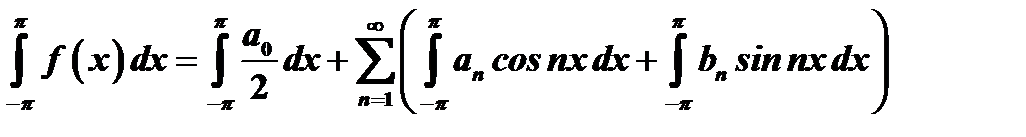
Вычислим отдельно каждый интеграл, встречающийся в правой части:

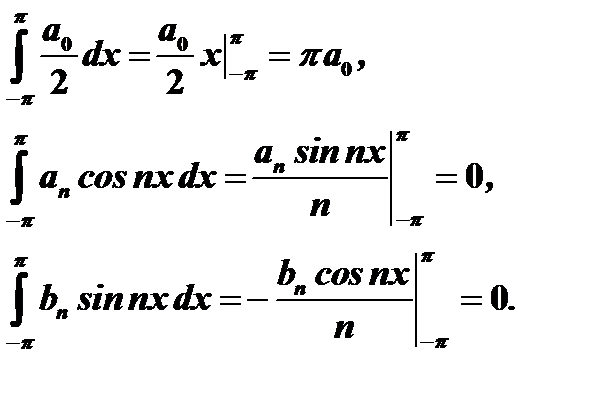
Следовательно, 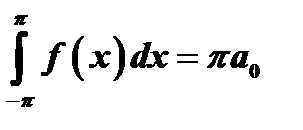, откуда

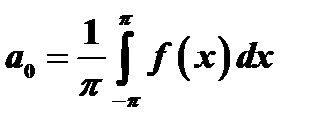(22)

Для вычисления остальных коэффициентов ряда нам потребуются некоторые определенные интегралы (доказать самостоятельно). Если и - целые числа, то имеют место следующие равенства:

если , то

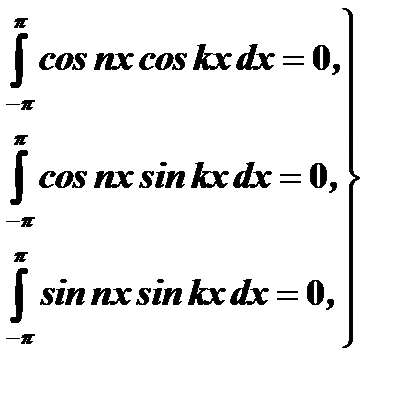(23)

если же 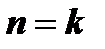, то

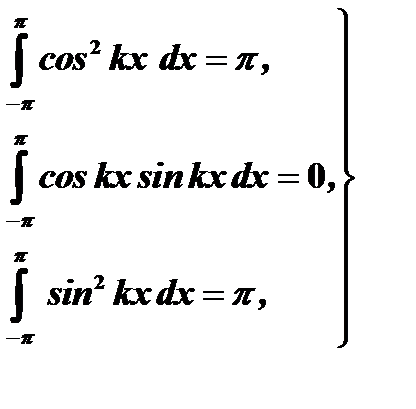(24)

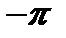Для определения коэффициента при каком-либо определенном значении умножим обе части равенства (21) на и проинтегрируем в пределах от до :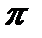

Принимая во внимание формулы (23) и (24), заметим, что все интегралы в правой части равны нулю, кроме интеграла с коэффициентом 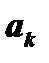. Следовательно,

,

откуда

(25)

Умножая обе части равенства (21) на 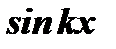и снова интегрируя в тех же пределах, получим:

,

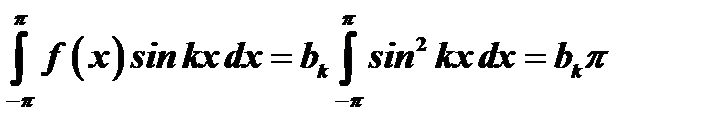откуда

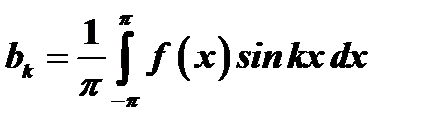(26)

Коэффициенты, определенные по формулам (22), (25), (26) называются коэффициентами Фурье функции , а тригонометрический ряд (20) с такими коэффициентами называется рядом Фурье функции .

Если периодическая функция с периодом 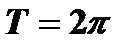- кусочно-монотонная и ограниченная на 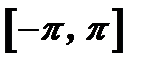, то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда 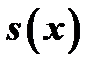равна значению функции в точках непрерывности функции. В точках разрыва функции сумма ряда равняется среднему арифметическому пределов функции справа и слева, т.е. если 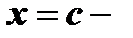точка разрыва функции , то

.

Периодическая функция обладает свойством , каково бы ни было число 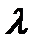, поэтому при вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования 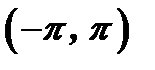промежутком интегрирования 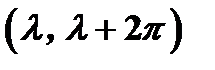, т.е.

(27)