Размещения без повторений
Определение. Размещениями из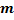 
элементов по 
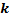называются такие соединения, каждое из которых содержит 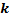элементов, взятых из данных 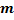элементов, и которые отличаются одно от другого или элементами, или порядком элементов и обозначается 
.
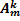Другими словами, если две выборки, отличающиеся только порядком записи символов, считают различными, то говорят о размещении из m элементов по k.
Пусть дано 
элементов: 
. Сначала составим из них все размещения по 1.
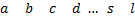
Их, очевидно, будет . Значит, 
.
Теперь составим все размещения по 2. Для этого к каждому из ранее составленных размещений по 1 приставим последовательно все оставшиеся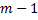 
элементов по 1. Так, к элементу 
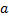приставим последовательно оставшиеся элементы: 
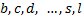; к элементу 
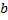приставим последовательно оставшиеся элементы: 
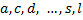и т.д. Получим следующие размещения по 2:
| m строк |
Так как всех элементов , то из каждого размещения по одному элементу мы получим 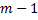размещений по 2, а всего их будет 
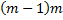. Значит, 
.
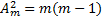Чтобы составить размещения по 3, берём каждое из составленных сейчас размещений по 2 и приставим к нему последовательно по одному все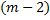 
оставшихся элементов. Тогда получим следующие размещения по 3:
| m(m-1) строк |
Так как число всех размещений по 2 равно m(m-1) и из каждого получается m-2 размещения по 3, то всех таких размещений окажется: m(m-1)(m-2). Таким образом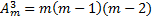 
. Подобно этому получим: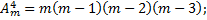 
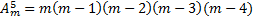, и вообще:
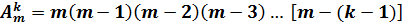
Числитель и знаменатель умножим на произведение 
.
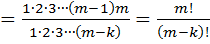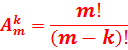
Дата добавления: 2015-12-29; просмотров: 590;