Сочетания с повторениями
Рассмотрим задачу. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоёные. Сколькими способами можно купить 7 пирожных?
Эта задача не является задачей на размещения с повторениями, так как порядок, в котором укладывают пирожные в коробку, несуществен. Задача ближе к задачам на сочетания. Но она отличается тем, что в комбинации могут входить повторяющиеся элементы, например, можно купить 7 эклеров. Такие задачи называют задачами на сочетания с повторениями.
Чтобы решить эту задачу, поступим следующим образом. Зашифруем каждую покупку с помощью нулей и единиц. Именно, сначала напишем столько единиц, сколько куплено наполеонов. Потом, чтобы отделить наполеоны от эклеров, напишем нуль, а затем – столько единиц, сколько куплено эклеров. Далее снова напишем нуль. Если не было куплено ни одного эклера, то в записи появятся два следующих друг за другом нуля. Далее напишем столько единиц, сколько куплено песочных пирожных, снова напишем нуль, и наконец, напишем столько единиц, сколько куплено слоёных пирожных. Например, если куплено 3 наполеона, 1 эклер, 2 песочных пирожных и 1 слоёное, то получим такую запись: 1110101101. Если же куплено 2 наполеона и 5 песочных, то получится запись: 1100111110.
Таким образом, число различных покупок равно числу перестановок с повторениями, которые можно составить из 7 единиц и 3 нулей. В результате получим:
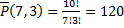 .
.
Общая формулировка таких задач такова: имеются предметы  различных типов. Сколько -комбинаций можно сделать из них, если не принимать во внимание порядок элементов в комбинации?
различных типов. Сколько -комбинаций можно сделать из них, если не принимать во внимание порядок элементов в комбинации?
Эта задача в общем виде решается точно так же, как и задача и пирожных. Именно, надо зашифровать каждую комбинацию с помощью нулей и единиц: для каждого типа написать столько единиц, сколько предметов этого типа входит в комбинацию, а различные типы отделять друг от друга нулями, при этом ели предметы какого-нибудь типа совсем не вошли в комбинацию, то надо писать подряд два или большее число нулей. При этом мы получим столько единиц, сколько предметов входит в комбинацию, т.е. 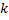 , а число нулей будет на 1 меньше, чем число типов предметов, т.е.
, а число нулей будет на 1 меньше, чем число типов предметов, т.е. 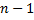 . Таким образом, мы получим перестановки с повторениями из
. Таким образом, мы получим перестановки с повторениями из 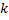 единиц и
единиц и 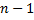 нулей.
нулей.
Число сочетаний с повторениями из элементов  типов обозначается
типов обозначается 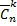 и равно числу перестановок с повторениями из
и равно числу перестановок с повторениями из 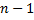 нулей и
нулей и 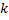 единиц. Таким образом:
единиц. Таким образом:
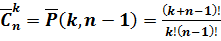 .
.
Заметим, что 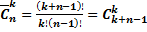 .
.
Дата добавления: 2015-12-29; просмотров: 840;
