Перестановки с повторениями
Переставляя буквы слова «ток», получим 6 различных перестановок:
ток тко отк окт кто кот
А если вместо слова «ток» взять слово «тот», то во всех выписанных перестановках надо будет заменить «к» на «т»
тот тто отт отт тто тот
При этом некоторые из наших перестановок окажутся одинаковыми и в итоге мы получим всего 3 различных перестановок.
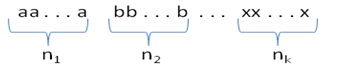 Общая задача формулируется следующим образом: имеются предметы
Общая задача формулируется следующим образом: имеются предметы 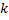 различных типов. Сколько перестановок можно сделать из
различных типов. Сколько перестановок можно сделать из 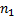 элементов первого типа,
элементов первого типа, 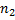 элементов второго типа, . . . ,
элементов второго типа, . . . , 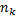 элементов
элементов 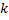 -го типа?
-го типа?
Число элементов в каждой перестановке равно 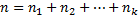 . Поэтому если бы все элементы были различны, то число перестановок равнялось бы
. Поэтому если бы все элементы были различны, то число перестановок равнялось бы  !. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В самом деле, возьмём, например, перестановку
!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В самом деле, возьмём, например, перестановку
в которой сначала выписаны все элементы первого типа, потом второго, . . . , наконец, 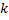 -го типа. Элементы первого типа можно переставлять друг с другом
-го типа. Элементы первого типа можно переставлять друг с другом 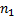 ! способами. Но так как все эти элементы одинаковы, то такие перестановки ничего не меняют. Точно так же ничего не меняют
! способами. Но так как все эти элементы одинаковы, то такие перестановки ничего не меняют. Точно так же ничего не меняют 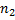 ! перестановок элементов второго типа и т.д. Поэтому множество всех
! перестановок элементов второго типа и т.д. Поэтому множество всех  ! перестановок распадается на части, состоящие из
! перестановок распадается на части, состоящие из 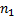 !
! 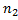 ! . . .
! . . . 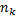 ! одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно
! одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно
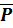 (
( 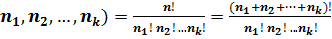
Дата добавления: 2015-12-29; просмотров: 751;
