Перестановки, инверсии, транспозиции.
Определение 1.Пусть 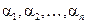 -
-  первых попарно различных натуральных чисел, т.е.
первых попарно различных натуральных чисел, т.е. 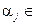 N,
N, 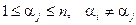 , если
, если 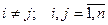 . Упорядоченный набор
. Упорядоченный набор 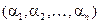 первых
первых  натуральных чисел будем называть перестановкой из
натуральных чисел будем называть перестановкой из  элементов.
элементов.
Перестановку 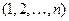 будем называть основной. Множество всех перестановок из
будем называть основной. Множество всех перестановок из  элементов будем обозначать так:
элементов будем обозначать так: 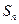 .
.
Пример 1. 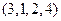 - перестановка из четырёх элементов.
- перестановка из четырёх элементов. 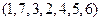 - перестановка из семи элементов.
- перестановка из семи элементов.
Теорема 1. Число различных перестановок из  элементов равно
элементов равно 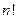 .
.
Доказательство проведём методом математической индукции по числу  .
.
База математической индукции.Пусть .Очевидно, существует единственная перестановка
.Очевидно, существует единственная перестановка 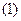 из одного элемента, т.е. для
из одного элемента, т.е. для  теорема верна.
теорема верна.
Индукционный переход. Докажем, что утверждение теоремы верно для перестановок из 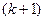 - го элемента, если оно верно для перестановок из
- го элемента, если оно верно для перестановок из 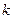 элементов.
элементов.
Множество всех перестановок из 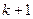 - го элемента разобьём на
- го элемента разобьём на 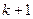 групп в зависимости от расположения в перестановке числа
групп в зависимости от расположения в перестановке числа 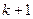 .
.
В 1 –ю группу включим все перестановки, в которых число 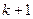 стоит на первом месте, т.е. перестановки вида
стоит на первом месте, т.е. перестановки вида 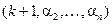 , в которых
, в которых 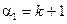 .
.
Во 2 –ю группу включим все перестановки, в которых число 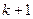 стоит на втором месте, т.е. перестановки вида
стоит на втором месте, т.е. перестановки вида 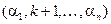 , в которых
, в которых 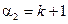 и т.д.
и т.д.
В 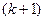 –ю группу включим все перестановки, в которых число
–ю группу включим все перестановки, в которых число 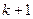 стоит на последнем месте, т.е. перестановки вида
стоит на последнем месте, т.е. перестановки вида 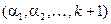 , в которых
, в которых 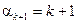 .
.
Подсчитаем, сколько перестановок содержится в каждой такой группе. Если мы из каждой перестановки, входящей в 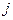 - ю группу, вычеркнем число
- ю группу, вычеркнем число 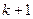 , то получившиеся перестановки будут образовывать всевозможные перестановки из
, то получившиеся перестановки будут образовывать всевозможные перестановки из 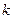 элементов, а их число по индукционному предположению равно
элементов, а их число по индукционному предположению равно 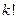 . Таким образом, получаем: число различных перестановок из
. Таким образом, получаем: число различных перестановок из 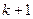 элементов равно
элементов равно 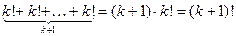 .
.
Дата добавления: 2015-12-01; просмотров: 1397;
