Свойства операции транспонирования.
Для любых матриц 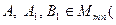 K
K 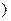 ,
, 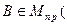 K
K 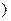 ,
, 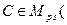 K
K 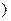 и любого числа
и любого числа
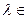 Kсправедливы равенства:
Kсправедливы равенства:
1. 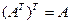 ;
;
2. 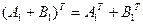 ;
;
3. 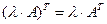 ;
;
4. 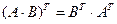 .
.
Доказательство.1. Из определения операции транспонирования следует, что в обеих частях равенства 1 стоят матрицы строения  на
на  . Сравним элементы этих матриц, стоящие на одинаковых местах:
. Сравним элементы этих матриц, стоящие на одинаковых местах:
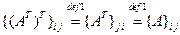 для всех
для всех 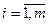 и
и 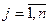 . Следовательно, по определению 8 справедливо равенство
. Следовательно, по определению 8 справедливо равенство 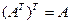 .
.
2. Из определений операций сложения и транспонирования матриц следует, что в обеих частях равенства 2 стоят матрицы строения  на
на  . Сравним элементы этих матриц, стоящие на одинаковых местах:
. Сравним элементы этих матриц, стоящие на одинаковых местах:
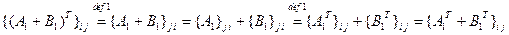 для всех
для всех 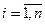 и
и 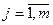 . Здесь мы воспользовались определением сложения матриц.
. Здесь мы воспользовались определением сложения матриц.
Следовательно, по определению 8 справедливо равенство 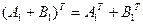 .
.
3. Из определений операций умножения матрицы на число и транспонирования матриц следует, что в обеих частях равенства 3 стоят матрицы строения  на
на  . Сравним элементы этих матриц, стоящие на одинаковых местах:
. Сравним элементы этих матриц, стоящие на одинаковых местах: 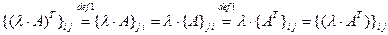 для всех
для всех 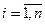 и
и 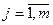 . Следовательно, по определению 8 справедливо равенство
. Следовательно, по определению 8 справедливо равенство 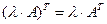 .
.
4. Из определений операций умножения матриц и транспонирования матриц следует, что в обеих частях равенства 4 стоят матрицы строения 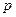 на
на  . Сравним элементы этих матриц, стоящие на одинаковых местах:
. Сравним элементы этих матриц, стоящие на одинаковых местах: 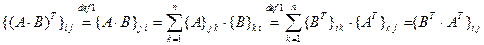
 для всех
для всех 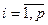 и
и 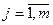 . Следовательно, по определению 8 справедливо равенство
. Следовательно, по определению 8 справедливо равенство 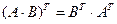 .
.
Дата добавления: 2015-12-01; просмотров: 1773;
