Определение 1.Пустьданы матрицы K и K ,причёмчисло столбцовматрицы равно числу строкматрицы .
Произведениемматрицы 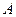 на матрицу
на матрицу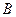 будем называть такую матрицу
будем называть такую матрицу 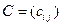 строения
строения  на
на 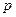 , элементы которой вычисляются по формуле
, элементы которой вычисляются по формуле  , или что то же самое
, или что то же самое 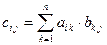 для всех
для всех 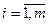 и
и  .
.
Обозначать матрицу 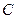 будем так:
будем так: 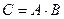 .
.
Заметим, что как следует из определения 1, произведение строки длины  на столбец высоты
на столбец высоты  имеет смысл. В результате получаем матрицу строения 1 на 1, т.е. число:
имеет смысл. В результате получаем матрицу строения 1 на 1, т.е. число:
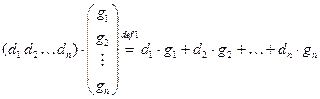
Пользуясь введёнными обозначениями элемент 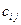 можно записать так:
можно записать так:
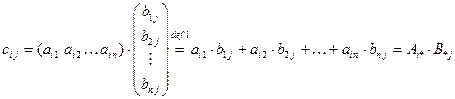 .
.
Таким образом, если 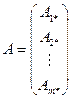 и
и 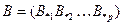 , то
, то

Пример 1. Если 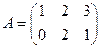 ,
, 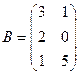 , то
, то 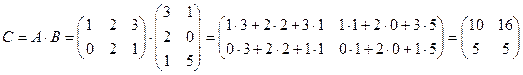
Замечание 1. Перемножать можно лишь такие матрицы, у которых число столбцов первой матрицы равно числу строк второй. Схематически это можно изобразить так:

Замечание 2. Из определения следует, что даже если произведение матриц 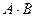 имеет смысл, то произведение
имеет смысл, то произведение  может не иметь смысла. Например,
может не иметь смысла. Например, 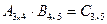 . Однако, произведение
. Однако, произведение
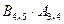 не имеет смысла, т.к.
не имеет смысла, т.к. 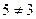 .
.
Даже если оба произведения имеют смысл и имеют одинаковое строение, то в общем случае 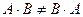 .
.
Например, 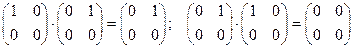 .
.
Замечание 3. В дальнейшем часто будем использовать введённое выше определение умножения матриц в случае, когда элементы одной матрицы – числа, а элементы другой – векторы, причём строение этих матриц согласовано так же, как в определении.
Пример 2. Например, 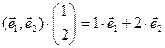 .
.
Пример 3. 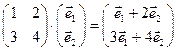
Дата добавления: 2015-12-01; просмотров: 951;
