Определение 2. Операцию, при которой меняются местами два элемента перестановки (не обязательно соседние), будем называть транспозицией.
Пример 2.Например: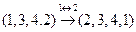 .В этой перестановке совершили одну транспозицию: поменяли местами 1 и 2.
.В этой перестановке совершили одну транспозицию: поменяли местами 1 и 2.
Определение 3. Если в перестановке 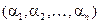 пара чисел
пара чисел 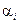 и
и 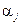 расположены так, что большее предшествует меньшему (т.е.
расположены так, что большее предшествует меньшему (т.е. 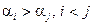 ), то говорят, что пара чисел
), то говорят, что пара чисел 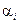 ,
, 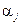 в этой перестановке образует инверсию(беспорядок.)
в этой перестановке образует инверсию(беспорядок.)
Пример 3.Например, в перестановке 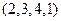 числа 2 и 1образуют инверсию, т.к.
числа 2 и 1образуют инверсию, т.к. 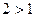 и 2 предшествует 1. В этой перестановке числа 4 и 1такжеобразуют инверсию.
и 2 предшествует 1. В этой перестановке числа 4 и 1такжеобразуют инверсию.
Определение 4. Число пар, образующих инверсию в данной перестановке, называется числом инверсий данной перестановки и обозначается так: 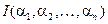 .
.
Определение 5. Перестановка называется чётной, если число инверсий этой перестановки чётное. Перестановка называется нечётной, если число инверсий этой перестановки нечётное.
Чтобы подсчитать число инверсных пар перестановки, подсчитаем сначала число пар, образующих инверсию, в состав которых входит 1.
Очевидно, таких пар столько, сколько чисел стоит перед единицей. Теперь подсчитаем число пар, образующих инверсию, в состав которых входит 2 (и не входит 1). Очевидно, таких пар столько, сколько не вычеркнутых чисел стоит перед двойкой, и т.д.
Пример 4.Подсчитаем количество инверсий в перестановке 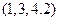 . Единица первая, следовательно, ни с одним из чисел инверсий не образует, и единицу вычёркиваем. Перед двойкой теперь стоят два не вычеркнутые числа. Следовательно, число 2 образует инверсию и с 3, и с 4, и двойку вычёркиваем. Перед тройкой не вычеркнутых чисел нет. Таким образом,
. Единица первая, следовательно, ни с одним из чисел инверсий не образует, и единицу вычёркиваем. Перед двойкой теперь стоят два не вычеркнутые числа. Следовательно, число 2 образует инверсию и с 3, и с 4, и двойку вычёркиваем. Перед тройкой не вычеркнутых чисел нет. Таким образом, 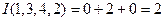 . Следовательно, перестановка
. Следовательно, перестановка 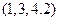 чётная.
чётная.
Без доказательства приведём следующую теорему.
Теорема 2.Транспозиция любых двух элементов перестановки меняет чётность перестановки на противоположную.
Следствие. Чётное число транспозиций не меняет чётность перестановки. Нечётное число транспозиций меняет чётность перестановки на противоположную.
Теорема 3. Число различных чётных перестановок из  элементов равно числу различных нечётных перестановок из
элементов равно числу различных нечётных перестановок из  элементов и равно
элементов и равно 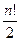 .
.
Доказательство. Обозначим через 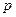 и
и 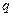 соответственно число различных чётных и нечётных перестановок из
соответственно число различных чётных и нечётных перестановок из  элементов. В каждой из
элементов. В каждой из
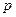 чётных перестановок поменяем местами первые два элемента. По теореме 2 все полученные таким образом перестановки являются нечётными, причём различными. Следовательно,
чётных перестановок поменяем местами первые два элемента. По теореме 2 все полученные таким образом перестановки являются нечётными, причём различными. Следовательно, 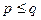 . Аналогично доказываем, что
. Аналогично доказываем, что 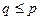 , откуда и получаем:
, откуда и получаем: 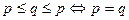 .
.
Тогда 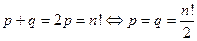 .
.
Дата добавления: 2015-12-01; просмотров: 1158;
