Теорема 2. Критерий существования обратной матрицы.
Для того чтобы для квадратной матрицы  существовала обратная матрица, необходимо и достаточно, чтобы её определитель был отличен от нуля.
существовала обратная матрица, необходимо и достаточно, чтобы её определитель был отличен от нуля.
Доказательство. Необходимость. Пусть для матрицы  существует обратная матрица
существует обратная матрица  . Тогда из определения 1 получаем:
. Тогда из определения 1 получаем: 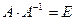 .
.
Следовательно, 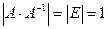 . Из теоремы об определителе произведения матриц следует, что
. Из теоремы об определителе произведения матриц следует, что 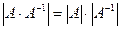 . Таким образом,
. Таким образом,
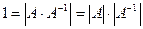 . Следовательно,
. Следовательно, 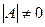 .
.
Достаточность. Пусть 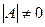 . Рассмотрим квадратную матрицу, которую обозначают так:
. Рассмотрим квадратную матрицу, которую обозначают так: 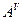 и называют присоединённой (или союзной) к матрице
и называют присоединённой (или союзной) к матрице  .
.
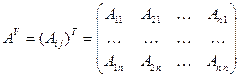 . Покажем, что
. Покажем, что 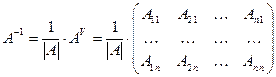 . Очевидно,
. Очевидно, 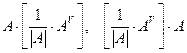
 K
K 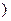 . Докажем, что
. Докажем, что 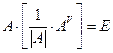 . Найдём элемент, стоящий в
. Найдём элемент, стоящий в 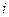 - ой строке и
- ой строке и 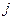 - ом столбце матрицы
- ом столбце матрицы 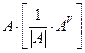 :
:
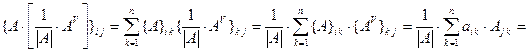
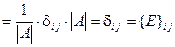 для всех
для всех 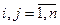 . Здесь мы воспользовались равенством (7)§8.
. Здесь мы воспользовались равенством (7)§8.
Следовательно, справедливо равенство 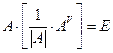 .
.
Аналогично предыдущему можно доказать равенство  , что предлагается сделать самостоятельно.
, что предлагается сделать самостоятельно.
Замечание. Из доказанного, в частности, следует, что для любой квадратной матрицы (не только неособенной) справедливо равенство 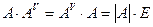 .
.
Пример. Найдём матрицу, обратную к матрице 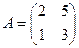 . Найдём определитель этой матрицы:
. Найдём определитель этой матрицы: 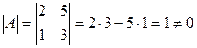 . Следовательно, матрица
. Следовательно, матрица  неособенная, и для неё существует обратная. Найдём алгебраические дополнения всех её элементов:
неособенная, и для неё существует обратная. Найдём алгебраические дополнения всех её элементов: 
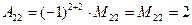 . Следовательно,
. Следовательно, 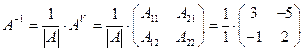 .
.
Продемонстрируем ещё один способ нахождения обратной матрицы, называемый методом Гаусса. Обоснование этого метода будет дано позже.
Выпишем расширенную матрицу 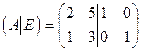 . Действуя только над строками этой матрицы добьёмся того, чтобы слева от черты оказалась единичная матрица. Тогда справа от черты получим обратную матрицу
. Действуя только над строками этой матрицы добьёмся того, чтобы слева от черты оказалась единичная матрица. Тогда справа от черты получим обратную матрицу  .
.
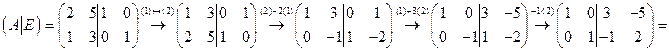
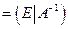 .
.
Дата добавления: 2015-12-01; просмотров: 5744;
