Простейшие свойства обратных матриц.
1. Если  - квадратная неособенная матрица, то справедливо равенство:
- квадратная неособенная матрица, то справедливо равенство: 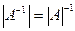 .
.
Доказывая необходимость теоремы 2, показали, что  , откуда и получаем равенство
, откуда и получаем равенство 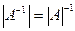 .
.
2. Если  - квадратная неособенная матрица, то для неё существует обратная матрица
- квадратная неособенная матрица, то для неё существует обратная матрица  и
и 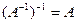 .
.
Доказательство. Из определения обратной матрицы следует, что 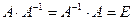 . Следовательно, по тому же определению 1 получаем:
. Следовательно, по тому же определению 1 получаем: 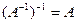 .
.
3. Если 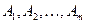 - квадратные неособенные матрицы одного порядка, то для матрицы
- квадратные неособенные матрицы одного порядка, то для матрицы 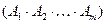 существует обратная матрица и
существует обратная матрица и
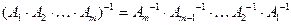 .
.
Доказательство. Рассмотрим произведение этих матриц: 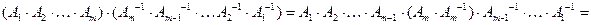
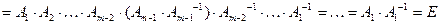 . Здесь мы воспользовались ассоциативностью умножения матриц и свойством единичной матрицы (свойства 1 и 5).
. Здесь мы воспользовались ассоциативностью умножения матриц и свойством единичной матрицы (свойства 1 и 5).
Аналогично проверяется, что произведение этих матриц в обратном порядке равно единичной матрице, что и доказывает равенство
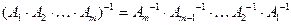 .
.
4. Если  - квадратная неособенная матрица, то существует матрица, обратная к матрице
- квадратная неособенная матрица, то существует матрица, обратная к матрице 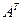 и
и 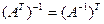 .
.
Доказательство. Из определения обратной матрицы следует, что 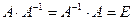 . Тогда по свойству 4 операции транспонирования получаем:
. Тогда по свойству 4 операции транспонирования получаем: 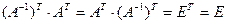 . Следовательно, по определению обратной матрицы
. Следовательно, по определению обратной матрицы 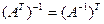 .
.
Теорема Крамера.
Теорема 2 §9 позволяет получить важные в теоретических приложениях формулы для решения квадратных систем линейных алгебраических уравнений.
Определение 1. Систему уравнений вида
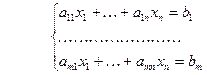 (1)
(1)
будем называть системой из 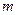 линейных алгебраических уравнений от
линейных алгебраических уравнений от  неизвестных
неизвестных 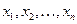 .
.
Числа 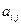 будем называть коэффициентами системы,
будем называть коэффициентами системы, 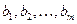 - свободными членами.
- свободными членами.
Матрицу 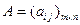 будем называть матрицей системы (1), столбец
будем называть матрицей системы (1), столбец 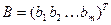 - столбцом свободных членов системы (1), столбец
- столбцом свободных членов системы (1), столбец 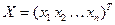 - столбцом неизвестных.
- столбцом неизвестных.
Очевидно, произведение 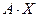 имеет смысл. Подсчитаем его:
имеет смысл. Подсчитаем его: 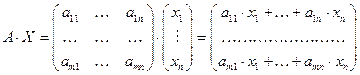 .
.
Из определения равенства матриц следует, что система (1) равносильна матричному равенству
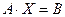 (2).
(2).
Равенство (2) будем называть матричной записью системы (1). Если 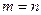 , т.е. число уравнений равно числу неизвестных, то систему (1) будем называть квадратной.
, т.е. число уравнений равно числу неизвестных, то систему (1) будем называть квадратной.
Определение 2. Решением системы (1) будем называть упорядоченный набор чисел 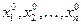 , удовлетворяющих равенствам (1), т.е. такой набор, для которого справедливы равенства
, удовлетворяющих равенствам (1), т.е. такой набор, для которого справедливы равенства
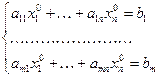 .
.
Этот упорядоченный набор чисел будем записывать в столбец 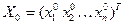 .
.
Таким образом, 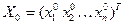 - решение системы (1)
- решение системы (1) 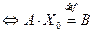
Дата добавления: 2015-12-01; просмотров: 1065;
