Свойства определителей.
I.Определитель матрицы равен определителю транспонированной к ней матрицы, т.е. 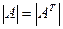 .
.
Это свойство приводится без доказательства.
Следствие. В силу свойства I все свойства определителей, справедливые для строк, справедливы и для столбцов и наоборот.
II.Еслив квадратной матрице поменять местами две строки (столбца), то её определитель изменит знак на противоположный, т.е. если 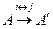 , то
, то 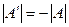 .
.
Это свойство приводится без доказательства.
III. Определитель, матрица которого имеет две одинаковые строки (столбца), равен нулю.
Доказательство. Пусть матрица 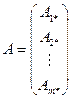 и
и 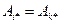 . Поменяем в матрице
. Поменяем в матрице 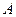
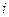 - ю и
- ю и 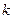 - ю строки.
- ю строки.
В результате мы получили матрицу 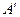 , которая равна матрице
, которая равна матрице 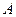 , т.к.
, т.к. 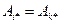 . По предыдущему свойству
. По предыдущему свойству
 . Следовательно,
. Следовательно, 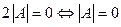 .
.
Пример. 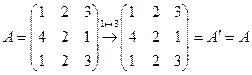 .
.
IY.Если всеэлементы какой-либо строки (столбца) матрицы определителя имеют общий множитель, то этот общий множитель можно вынести за знак определителя, т.е. 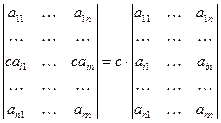 .
.
Элементы, обозначенные точками и стоящие на одинаковых местах, кроме элементов 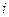 - ой строки, в обоих определителях равны.
- ой строки, в обоих определителях равны.
Доказательство. Из определения определителя получаем:

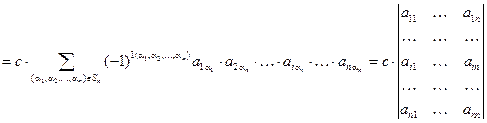 .
.
Следствие. Определитель матрицы, содержащей нулевую строку (столбец), равен нулю.
Доказательство.Действительно, в этом случае можно считать, что общим множителем элементов нулевой строки является 0. Применяя доказанное свойство, получаем, что такой определитель равен нулю.
Y.Определитель матрицы, содержащей две пропорциональные строки (два пропорциональные столбца), равен нулю.
Доказательство. 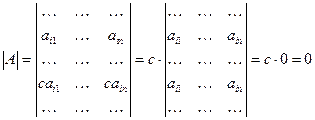
Здесь мы воспользовались свойствами IY и III.
YI.Если все элементы какой-либо строки (столбца) матрицы определителя представлены в виде суммы двух слагаемых, то определитель этой матрицы равен сумме двух определителей, в первом из которых элементы отмеченной строки (отмеченного столбца) равны первым слагаемым, а во втором – вторым. Элементы всех остальных строк (столбцов), стоящие на одинаковых местах, во всех трёх определителях равны, т.е.
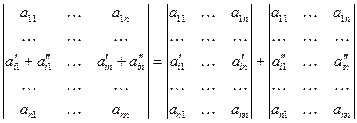 .
.
Доказательство. Из определения определителя получаем:
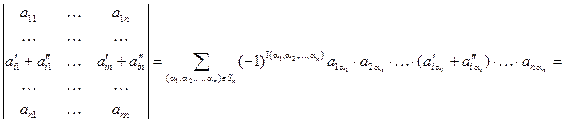
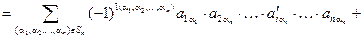
 .
.
YII.Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) добавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, т.е.
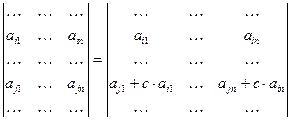
Элементы всех остальных строк, стоящие на одинаковых местах, в обоих определителях равны.
Доказательство. Из свойства YI определителя получаем:
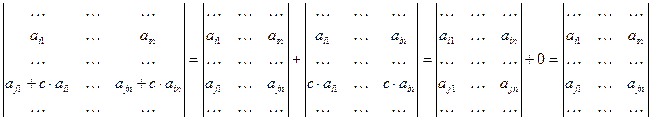 , т.к. по свойству Y определитель, матрица которого содержит две пропорциональные строки, равен нулю.
, т.к. по свойству Y определитель, матрица которого содержит две пропорциональные строки, равен нулю.
Для того чтобы сформулировать следующие свойства определителя, нам понадобятся новые определения.
Определение 1. Минором элемента 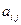 в определителе
в определителе 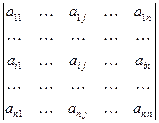 будем называть определитель, матрица которого получается из матрицы исходного в результате вычёркивания
будем называть определитель, матрица которого получается из матрицы исходного в результате вычёркивания 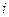 - ой строки и
- ой строки и 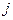 - го столбца. Обозначать минор элемента
- го столбца. Обозначать минор элемента 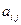 будем так:
будем так: 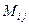
Алгебраическим дополнениемэлемента 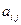 в том же определителе будем называть число, равное
в том же определителе будем называть число, равное 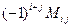 . Обозначать алгебраическое дополнение будем так:
. Обозначать алгебраическое дополнение будем так: 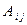 , т.е.
, т.е. 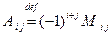 .
.
Замечание. Очевидно, минор и алгебраическое дополнение элемента 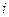 - ой строки и
- ой строки и 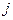 - го столбца, т.е.
- го столбца, т.е. 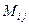 и
и 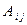 не зависят от элементов
не зависят от элементов 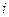 - ой строки и
- ой строки и 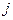 - го столбца.
- го столбца.
Пример 1. Пусть дан определитель 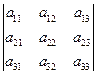 . Найдём минор
. Найдём минор 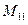 и алгебраическое дополнение
и алгебраическое дополнение 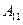 элемента
элемента  в этом определителе:
в этом определителе: 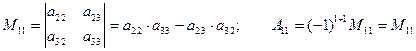 .
.
Теперь найдём минор  и алгебраическое дополнение
и алгебраическое дополнение 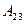 элемента
элемента 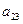 в этом определителе:
в этом определителе:
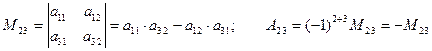 .
.
Без доказательства приведём следующее свойство определителей.
YIII.Определитель матрицы равен сумме произведений элементов какой- либо строки (столбца) на их алгебраические дополнения, т.е.
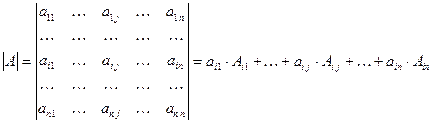 (1)
(1)
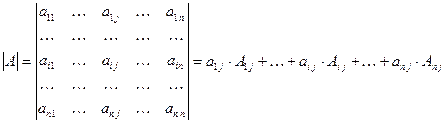 (2)
(2)
Замечание. Равенство (1) называют разложением определителя по элементам 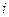 - ой строки. Равенство (2) называют разложением определителя по элементам
- ой строки. Равенство (2) называют разложением определителя по элементам 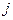 - го столбца.
- го столбца.
IX.Пусть дан определитель 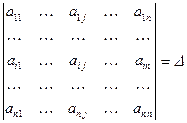 и
и  чисел
чисел 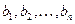 .Сумма произведений этих чисел на алгебраические дополнения элементов
.Сумма произведений этих чисел на алгебраические дополнения элементов 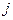 - ой строки (
- ой строки ( 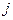 - го столбца) равна определителю, матрица которого получается из матрицы исходного в результате замены элементов
- го столбца) равна определителю, матрица которого получается из матрицы исходного в результате замены элементов 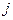 - ой строки (
- ой строки ( 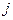 - го столбца) на числа
- го столбца) на числа 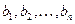 соответственно, т.е.
соответственно, т.е.
 (3)
(3)
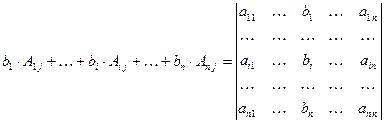 (4)
(4)
Докажем равенство (4). Разложим определитель 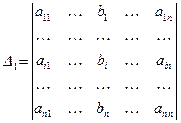 по элементам
по элементам 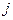 - го столбца. Алгебраическое дополнение элемента
- го столбца. Алгебраическое дополнение элемента 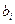 в определителе
в определителе 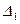 будем обозначать так:
будем обозначать так: 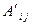 . Из свойства YIII, получим:
. Из свойства YIII, получим: 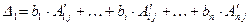 (разложение определителя
(разложение определителя 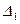 по элементам
по элементам 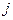 - го столбца). Заметим, что матрицы определителей
- го столбца). Заметим, что матрицы определителей 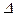 и
и 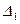 отличаются только элементами
отличаются только элементами 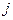 - го столбца, но в силу замечания после определения 1 алгебраические дополнения
- го столбца, но в силу замечания после определения 1 алгебраические дополнения 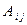 и
и 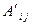 не зависят от элементов
не зависят от элементов 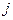 - го столбца. Следовательно,
- го столбца. Следовательно,  для всех
для всех 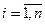 и
и 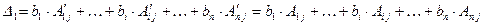 .
.
X.Сумма произведений элементов какой-либо строки (столбца) матрицы определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) этого же определителя равна нулю, т.е.
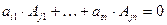 , если
, если 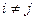 ; (5)
; (5)
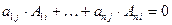 , если
, если 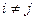 (6)
(6)
Докажем равенство (5). Используем свойство IX. Заменим в матрице определителя 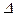 элементы
элементы 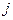 - ой строки числами
- ой строки числами 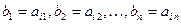 . Тогда по свойству IX получим:
. Тогда по свойству IX получим:
 , т.к. матрица последнего определителя содержит две одинаковые строки и, следовательно, по свойству III её определитель равен нулю.
, т.к. матрица последнего определителя содержит две одинаковые строки и, следовательно, по свойству III её определитель равен нулю.
Запишем равенства (1) и (5): 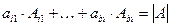 (1)
(1)
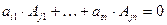 , если
, если 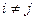 ; (5).
; (5).
Используя символ Кронекера оба эти равенства можно записать так:
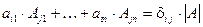 (7)
(7)
Очевидно, если 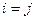 , то из равенства (7) получаем равенство (1). Если
, то из равенства (7) получаем равенство (1). Если 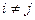 , то из равенства (7) получаем равенство (5).
, то из равенства (7) получаем равенство (5).
Равенство 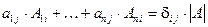 (8) является обобщением равенств (2) и (6).
(8) является обобщением равенств (2) и (6).
В заключение этого параграфа приведём без доказательства следующую теорему.
Дата добавления: 2015-12-01; просмотров: 3128;
