Определение 2.Матрицу будем называть квадратной, если . В этом случае число будем называть порядком матрицы.
Определители и матрицы.
Определения и обозначения.
Определение 1. Матрицей будем называть прямоугольную таблицу, заполненную математическими объектами одинакового типа, как правило, числами.
Матрицы обычно будем обозначать большими буквами латинского алфавита или записывать в развёрнутом виде:
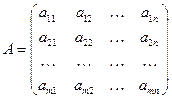 .
.
Про такую матрицу будем говорить, что она имеет строение 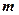 на
на 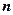 (запись
(запись 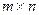 ), т.е. в матрице
), т.е. в матрице 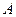
 горизонтальных рядов (строк) и
горизонтальных рядов (строк) и  вертикальных рядов (столбцов).
вертикальных рядов (столбцов).
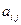 называют элементами матрицы
называют элементами матрицы 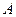 . Индексы
. Индексы 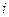 и
и 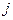 означают, что элемент
означают, что элемент 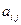 стоит в
стоит в 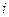 - ой строке и в
- ой строке и в 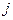 - ом столбце. Иногда удобно элемент матрицы
- ом столбце. Иногда удобно элемент матрицы 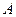 , стоящий в
, стоящий в 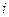 - ой строке и в
- ой строке и в 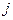 - ом столбце обозначать так:
- ом столбце обозначать так: 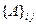 .
.
В некоторых случаях матрицу 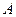 будем кратко записывать так:
будем кратко записывать так: 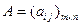 или так:
или так: 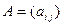 .
.
Множество всех матриц строения  на
на  с элементами в поле Kбудем обозначать так:
с элементами в поле Kбудем обозначать так: 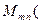 K
K 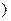 .
.
Например, множество всех матриц строения  на
на  , элементами которых являются вещественные числа, будем обозначать так:
, элементами которых являются вещественные числа, будем обозначать так: 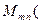 R
R 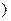 .
.
Определение 2.Матрицу будем называть квадратной, если . В этом случае число будем называть порядком матрицы.
В общем случае матрица называется прямоугольной. Множество всех квадратных матриц порядка  с элементами в поле K будем обозначать так:
с элементами в поле K будем обозначать так: 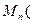 K
K 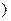 .
.
Множество всех матриц строения 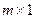 , т.е. столбцов высоты
, т.е. столбцов высоты  с элементами в поле K,будем обозначать так:K
с элементами в поле K,будем обозначать так:K 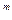 , т.е. K
, т.е. K 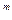
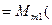 K
K 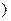 .
.
Множество всех матриц строения 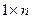 , т.е. строк длины
, т.е. строк длины  с элементами в поле K,будем обозначать так:K
с элементами в поле K,будем обозначать так:K 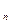 , т.е. K
, т.е. K 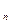
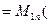 K
K 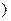 .
.
Определение 3.Совокупность элементов 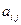 матрицы
матрицы 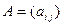 , для которых
, для которых 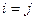 , будем называть главной диагональю, соответствующие элементы
, будем называть главной диагональю, соответствующие элементы 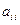 - диагональными, остальные элементы – внедиагональными.
- диагональными, остальные элементы – внедиагональными.
Определение 4. Квадратную матрицу будем называть диагональной, если все её внедиагональные элементы равны нулю.
Диагональную матрицу с элементами 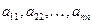 будем обозначать так:
будем обозначать так: 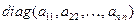 .
.
Дата добавления: 2015-12-01; просмотров: 817;
