Свойства сложения матриц и умножения матрицы на число.

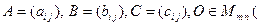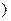Для любых матриц K и для любых чисел 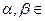Kсправедливы равенства:

1. 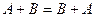(коммутативность сложения);

2. 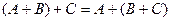(ассоциативность сложения);

3. ;

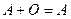4. ;

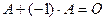Матрицу 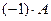далее будем обозначать так: 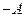и называть противоположной к ;

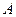5 . ;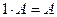

6. 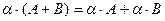(дистрибутивность относительно сложения матриц);

7. 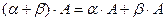(дистрибутивность относительно сложения чисел);

8. .

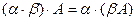Доказательство.Из определений 1 и 2 следует, что все матрицы в равенствах 1-8 имеют одинаковое строение на . Следовательно, нужно доказать, что в каждом из этих равенств в обеих частях на одинаковых местах стоят равные элементы.

1. 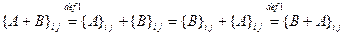для всех 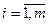и 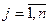, т.к. сложение чисел коммутативно. Следовательно, по определению 8 справедливо равенство .

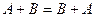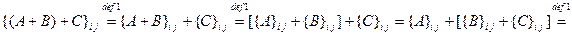
2. 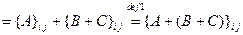для всех 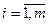и 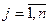, т.к. сложение чисел ассоциативно. Следовательно, по определению 8 справедливо равенство .

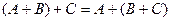3. 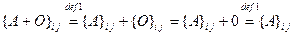для всех 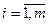и 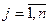. Следовательно, по определению 8 справедливо равенство .

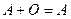4. 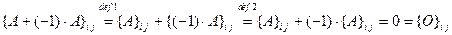для всех 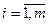и 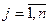. Следовательно, по определению 8 справедливо равенство .

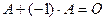5. 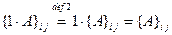для всех 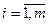и 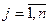. Следовательно, по определению 8 справедливо равенство .

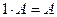6.

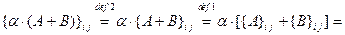
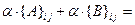
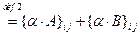
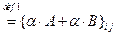для всех 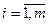и 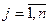, т.к. сложение и умножение чисел обладают свойством дистрибутивности. Следовательно, по определению 8 справедливо равенство .

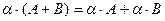7.

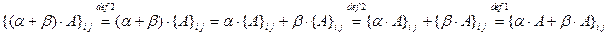
для всех 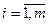и 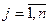, т.к. сложение и умножение чисел обладают свойством дистрибутивности. Следовательно, по определению 8 справедливо равенство .

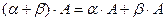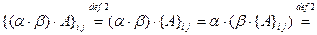
8. 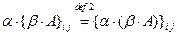для всех 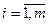и 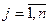, т.к. умножение чисел ассоциативно. Следовательно, по определению 8 справедливо равенство .

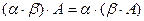Умножение матриц.