Функциональные ряды. Ряд называется функциональным, если его члены являются функциями от .

Ряд 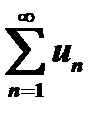называется функциональным, если его члены являются функциями от .

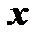Рассмотрим функциональный ряд 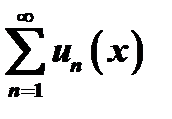. Давая 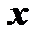определенные числовые значения, получим различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Совокупность тех значений 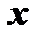, при которых функциональный ряд сходится, называют областью сходимости этого ряда. Очевидно, что в области сходимости ряда его сумма является некоторой функцией от 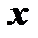. Поэтому сумму функционального ряда обозначают через .

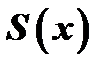Среди функциональных рядов наиболее распространенным является степенной ряд.

Степенным рядом называется ряд вида 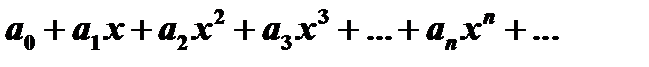, (9)

где 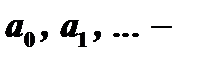постоянные числа, называемые коэффициентами ряда.

При каждом фиксированном значении переменной степенной ряд превращается в некоторый числовой ряд. Если полученный для какого-то значения 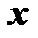числовой ряд оказывается сходящимся, то говорят, что при этом значении 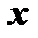, или в этой точке степенной ряд сходится. Если же для другого значения соответствующий числовой ряд окажется расходящимся, то говорят, что степенной ряд в такой точке расходится. Совокупность значений 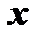, при которых заданный степенной ряд сходится, называется областью сходимости степенного ряда. Область сходимости степенного ряда является интервалом числовой оси, симметричным относительно точки .

Определение интервала сходимости степенного ряда строится на подчинении значений 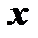условию сходимости числового ряда. Если все коэффициенты степенного ряда отличны от нуля, то применение для этой цели признака Даламбера приводит к неравенству

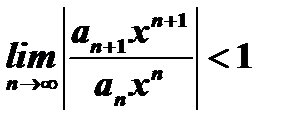. (10)

Знак абсолютного значения связан с тем, что коэффициенты степенного ряда и значения переменной 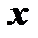могут быть как положительными, так и отрицательными числами. Условие (10) после преобразования принимает вид

,

откуда

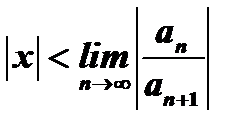. (11)

Неотрицательное число, определяемое этим пределом (если он существует), называется радиусом сходимости степенного ряда и обозначается символом 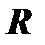. Таким образом, радиус сходимости степенного ряда

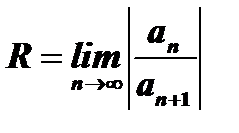. (12)

Знак абсолютной величины для тех значений 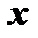, при которых степенной ряд сходится (11), позволяет определить интервал сходимости в виде . Этим охватывается совокупность и положительных и отрицательных значений 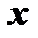, при которых степенной ряд сходится.

В соответствии с возможными значениями предела (12) различаются три случая для интервала сходимости степенного ряда.

1. При интервал сходимости степенного ряда является множество всех действительных чисел.

2. При 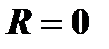интервал сходимости вырождается в точку 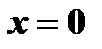, и соответствующий ряд сходится к своему свободному члену.

3. При конечном значении 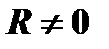интервал сходимости степенного ряда является ограниченным, - при значениях 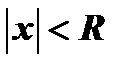, т.е. внутри этого интервала, соответствующий ряд сходится, а при , т.е. вне интервала сходимости, ряд расходится.

На концах интервала сходимости степенной ряд может сходиться, а может и расходиться. Уточнение этого вопроса связано с исследованием сходимости числовых рядов, в которые обращается заданный степенной ряд при и при .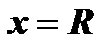

Степенным рядом также называется функциональный ряд вида

Этот ряд сходится при значениях 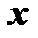, удовлетворяющих неравенству .