Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда
Числовым рядом называется выражение вида
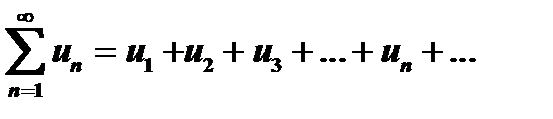 (5),
(5),
где 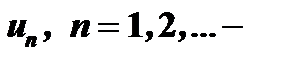 члены ряда,
члены ряда, 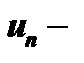 общий член ряда (5).
общий член ряда (5).
Сумма 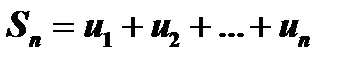 первых
первых  членов ряда (5) называется частичной суммой этого ряда.
членов ряда (5) называется частичной суммой этого ряда.
Суммой  ряда называется предел частичной суммы
ряда называется предел частичной суммы 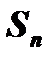 этого ряда при условии, что
этого ряда при условии, что 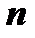 произвольным способом неограниченно возрастает:
произвольным способом неограниченно возрастает:
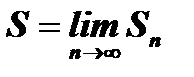 (6)
(6)
Числовой ряд, имеющий сумму в смысле этого определения, называется сходящимся, ряд же, не имеющий суммы, называется расходящимся.
Отметим некоторые свойства сходящихся рядов:
1. Если в сходящемся ряде заменить конечное число членов новыми числами, или отбросить или приписать конечное число членов ряда, или совершить перестановку любого конечного числа членов ряда, то получим новый сходящийся ряд.
2. Если все члены сходящегося ряда, сумма которого равна 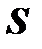 , умножить на некоторое число
, умножить на некоторое число 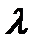 , то получится новый сходящийся ряд, сумма которого равна
, то получится новый сходящийся ряд, сумма которого равна  .
.
3. Сумма и разность двух сходящихся рядов есть новый сходящийся ряд. Его сумма равна соответственно сумме или разности сумм этих двух рядов.
Необходимый признак сходимости ряда. Теорема. Если ряд сходится, то его 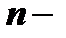 ый член стремится к нулю при неограниченном возрастании
ый член стремится к нулю при неограниченном возрастании 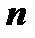 , т.е.
, т.е. 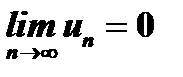 .
.
Доказательство. Пусть ряд (5) сходится, т.е. 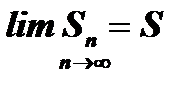 , тогда имеет место также и равенство
, тогда имеет место также и равенство 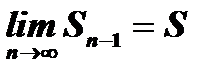 . Вычитая почленно из первого равенства второе, получим
. Вычитая почленно из первого равенства второе, получим 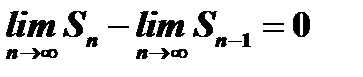 или
или  . Но
. Но 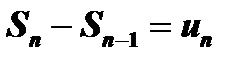 , следовательно
, следовательно 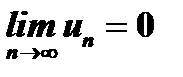 .
.
Следствие. Если 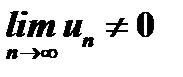 , то ряд расходится.
, то ряд расходится.
Рассмотренный признак является только необходимым, но не является достаточным, т.е. из того, что 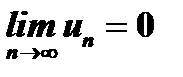 , еще не следует, что ряд сходится, - ряд может и расходиться. Так, например, так называемый гармонический ряд
, еще не следует, что ряд сходится, - ряд может и расходиться. Так, например, так называемый гармонический ряд 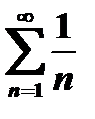 расходится, хотя
расходится, хотя  . Покажем это. Пусть
. Покажем это. Пусть 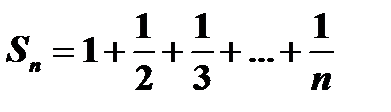 ,
, 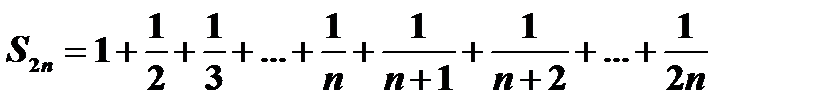 , поэтому
, поэтому 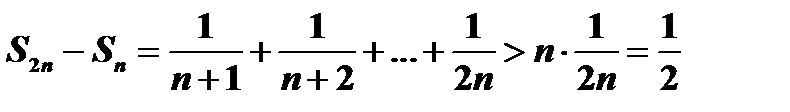 , или
, или 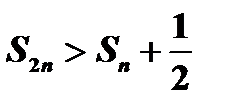 . Если бы гармонический ряд сходился, то по определению
. Если бы гармонический ряд сходился, то по определению 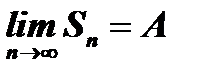 , а тогда последовательность
, а тогда последовательность 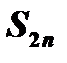 имела бы тот же предел
имела бы тот же предел 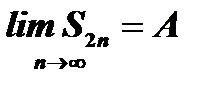 , а в предшествующем неравенстве был бы возможен предельный переход, который привел бы к соотношению
, а в предшествующем неравенстве был бы возможен предельный переход, который привел бы к соотношению 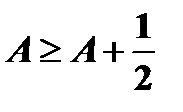 , что нелепо.
, что нелепо.
Дата добавления: 2015-12-29; просмотров: 759;
