Системы линейных дифференциальных уравнений с постоянными коэффициентами

Пусть дана система дифференциальных уравнений

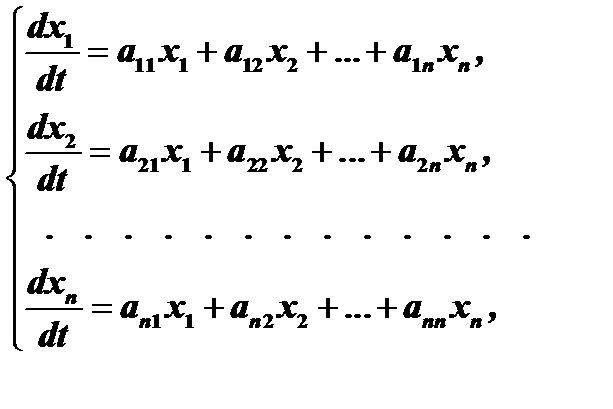( 1 )

где 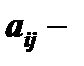постоянные, 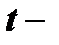аргумент, 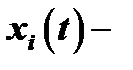искомые функции, 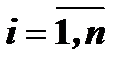. Система (1) называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.

Эту систему можно решать путём сведения к одному уравнению 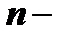го порядка, которое в данном случае будет линейным. Но можно решать систему (1) и другим методом, не сводя к уравнению 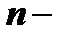го порядка. Этот метод даёт возможность более наглядно анализировать характер решений.

Будем искать решение системы в виде:

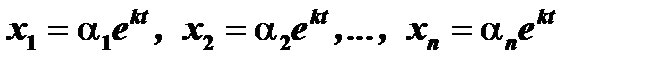( 2 )

Надо определить постоянные 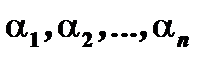и 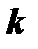так, чтобы функции 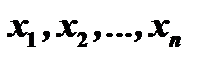удовлетворяли системе уравнений (1), т.е.

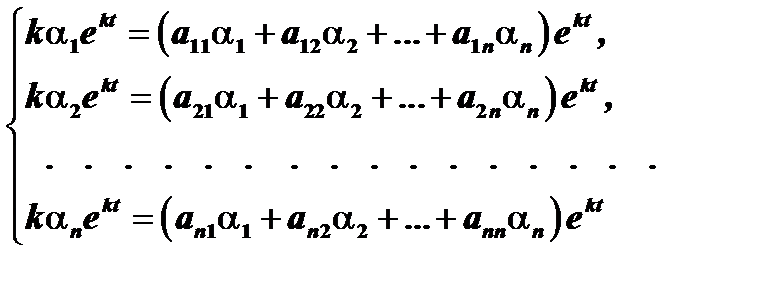
Сократив на 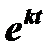, перенеся все члены в одну сторону и собрав коэффициенты при 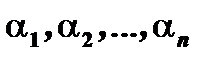, получим систему уравнений

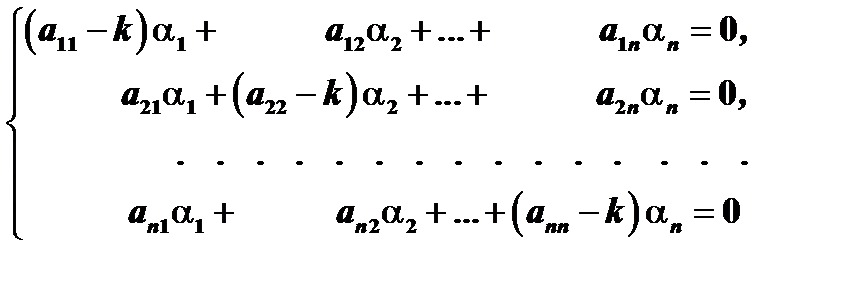( 3 )

Выберем 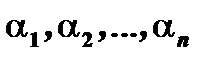и 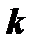такими, чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно 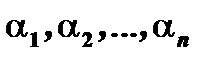. Из курса линейной алгебры следует, что она будет иметь нетривиальное решение, если

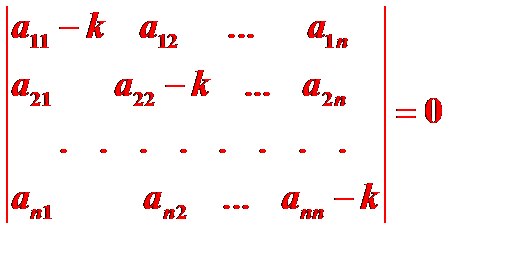( 4 )

Это уравнение называется характеристическим уравнением для системы (1), его корни называются корнями характеристического уравнения.

В качестве примера рассмотрим случай, когда корни характеристического уравнения 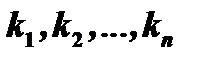- действительные и различные.

Для каждого корня 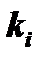напишем систему уравнений (3) и определим коэффициенты

.

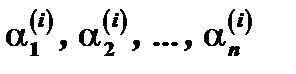Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:

для корня 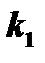решение системы (1)

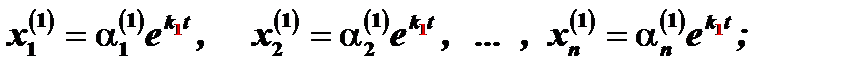
для корня 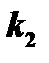решение системы (1)

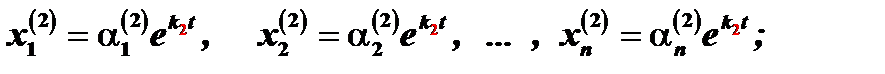
для корня 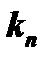решение системы (1)

.

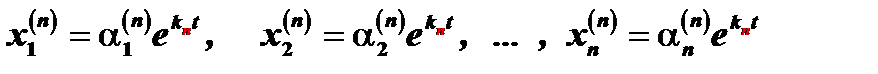Путём непосредственной подстановки в уравнения можно убедиться, что система функций

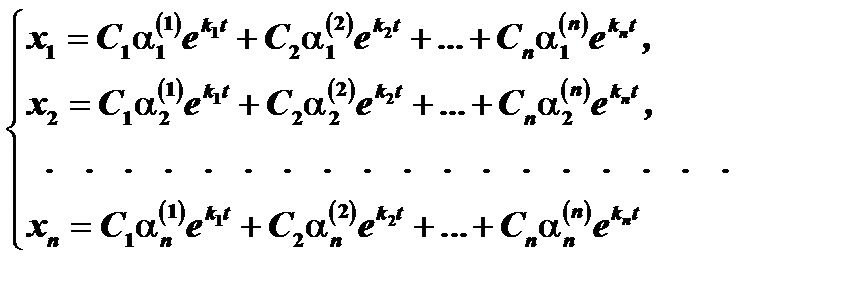( 5 )

где 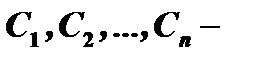произвольные постоянные, тоже является решением системы дифференциальных уравнений (1). Это есть общее решение системы (1)

Р Я Д Ы

Числовые ряды