Системы обыкновенных дифференциальных уравнений

Рассмотрим систему уравнений первого порядка

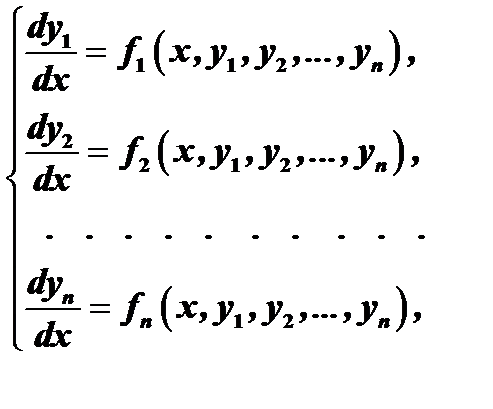( 1 )

где 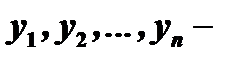искомые функции, 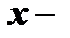аргумент.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Решить систему – значит определить функции 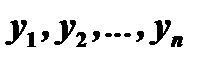, удовлетворяющие системе уравнений (1) и данным начальным условиям:

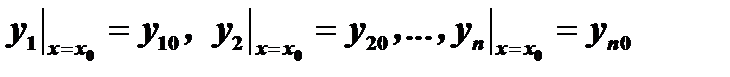( 2 )

Интегрирование системы (1) производится следующим образом.

Дифференцируем по 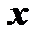первое из уравнений (1):

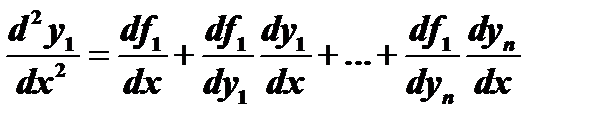
Заменяя производные 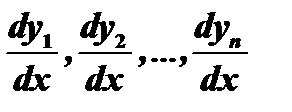их выражениями 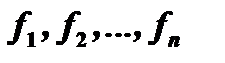из уравнений (1), будем иметь уравнение

.

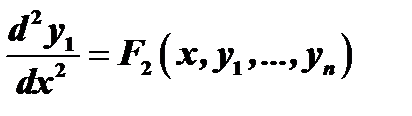Дифференцируя полученное уравнение и поступая аналогично предыдущему, получим:

.

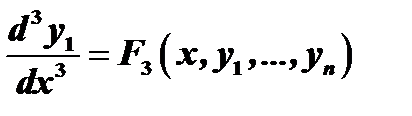Продолжая далее, таким же образом получим, наконец, уравнение

.

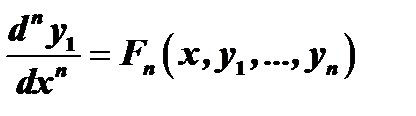Итак, получим следующую систему:

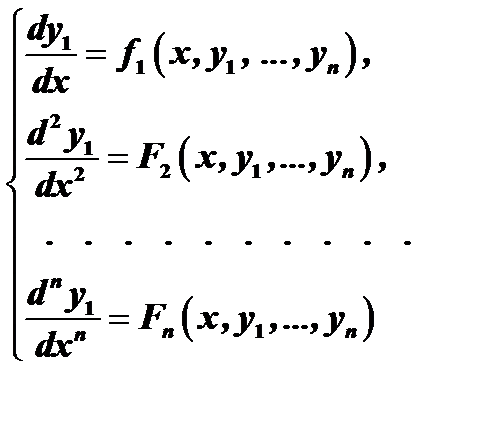( 3 )

Из первых 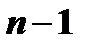уравнений определим 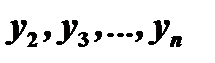выразив их через 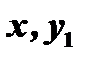и производные :

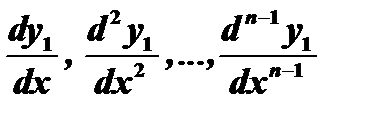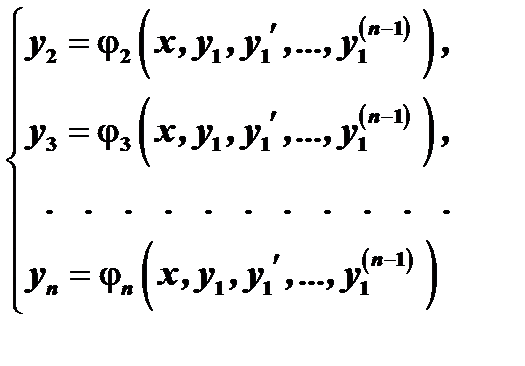( 4 )

Подставляя эти выражения в последнее из уравнений (3), получим уравнение 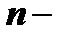порядка для определения :

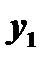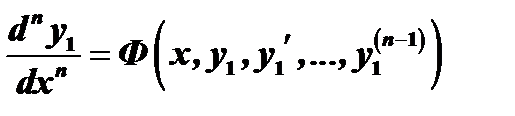. ( 5 )

Решая уравнение (5), определим :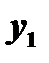

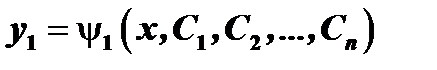( 6 )

Дифференцируя выражение (6) 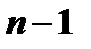раз, найдём производные

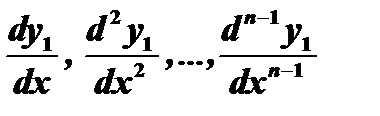
как функции от 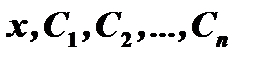. Подставляя эти функции в (4), получим :

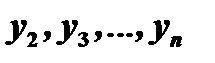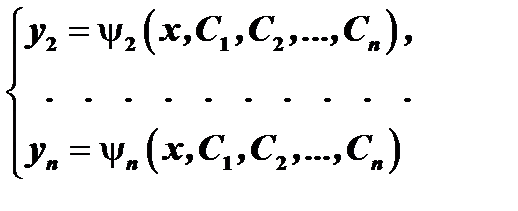( 7 )