Достаточные признаки сходимости рядов с положительными членами

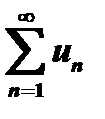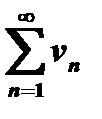1. Признак сравнения.Если даны два ряда и с неотрицательными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда: 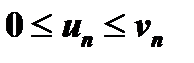, то:

а) из сходимости второго ряда следует сходимость первого ряда,

б) из расходимости первого ряда следует расходимость второго ряда.

Для сравнения часто используются ряды:

1) 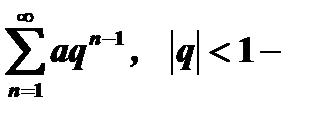сходящийся (геометрическая прогрессия),

2) ,

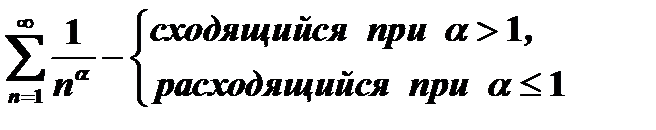3) есл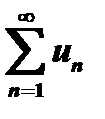и и 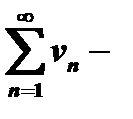ряды с положительными членами и существует конечный

,

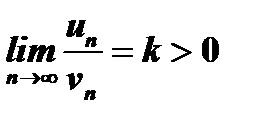то рассматриваемые ряды одновременно сходятся или расходятся.

Сходимость рядов вида 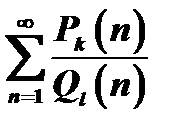, где 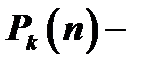многочлен степени 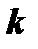, 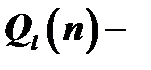многочлен степени 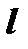, полностью исчерпывается сравнением с рядом 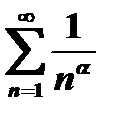, где .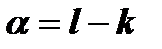

2. Признак Даламбера.Если ряд 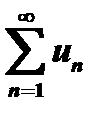с положительными членами таков, что существует 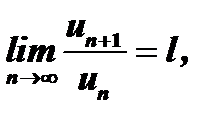то ряд сходится при 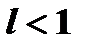и расходится при .

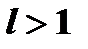Если 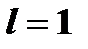, то вопрос о поведении ряда остается открытым.

3. Признак Коши. Если ряд 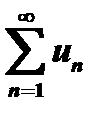с положительными членами таков, что существует 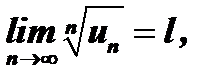то ряд сходится при 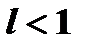и расходится при .

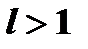Если 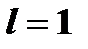, то вопрос о поведении ряда остается открытым.

4. Интегральный признак. Если функция 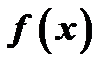непрерывная, положительная, невозрастающая для 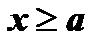и, начиная с некоторого 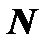, , 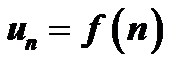то ряд 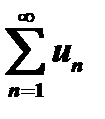и несобственный интеграл 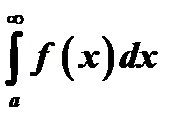одновременно сходятся или расходятся.