Неоднородные линейные уравнения второго порядка
Неоднородное линейное уравнение второго порядка имеет вид
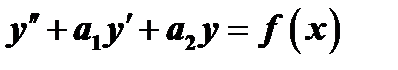
Общее решение данного уравнения определяется как сумма какого-нибудь частного решения этого уравнения 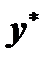 и общего решения
и общего решения 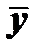 соответствующего однородного уравнения
соответствующего однородного уравнения
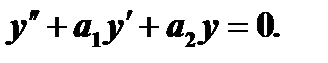

Так как общее решение 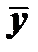 однородного уравнения
однородного уравнения 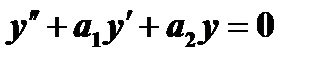 мы уже умеем находить, то основная задача при интегрировании неоднородного уравнения
мы уже умеем находить, то основная задача при интегрировании неоднородного уравнения 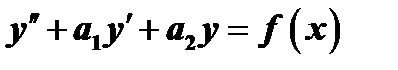 состоит в нахождении какого-нибудь его частного решения
состоит в нахождении какого-нибудь его частного решения 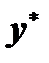 .
.
Укажем общий метод нахождения частных решений неоднородного уравнения, который называется методом вариации произвольных постоянных.
Общее решение однородного уравнения имеет вид 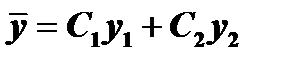 . Будем искать частное решение неоднородного уравнения
. Будем искать частное решение неоднородного уравнения 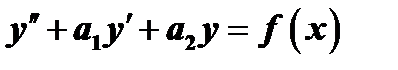 в такой же форме, предполагая
в такой же форме, предполагая 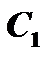 и
и 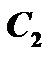 как некоторые пока неизвестные функции от
как некоторые пока неизвестные функции от 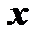 , т.е.
, т.е.
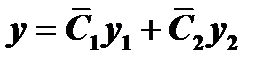 , (1)
, (1)
где 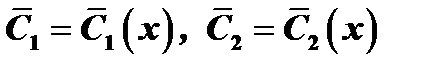 .
.
Продифференцируем равенство (1): 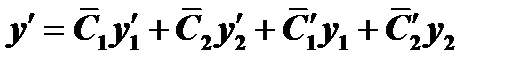 (2)
(2)
Подберём 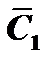 и
и 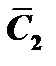 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство 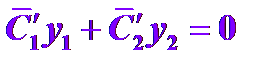 , тогда
, тогда 
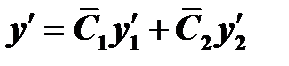 (3)
(3)
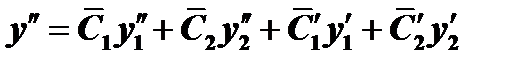 (4)
(4)
Подставляя (1), (3) и (4) в уравнение 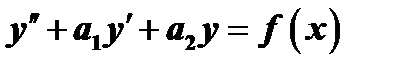 , получим
, получим
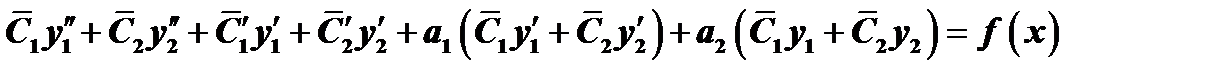 или
или
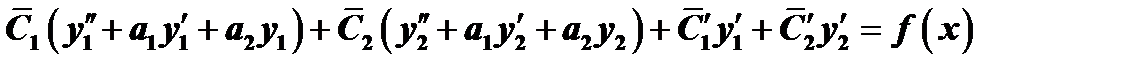
Т.к. 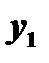 и
и 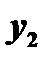 - решения однородного уравнения
- решения однородного уравнения 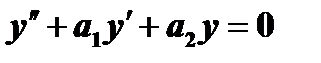 , то
, то 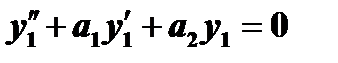 и
и 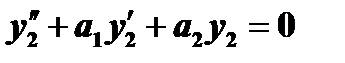 , следовательно
, следовательно 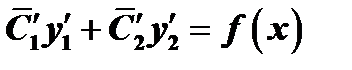 . Таким образом, выражение (1) будет решением неоднородного уравнения
. Таким образом, выражение (1) будет решением неоднородного уравнения 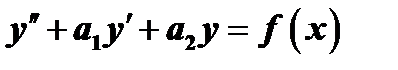 в том случае, если
в том случае, если 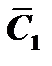 и
и 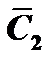 удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
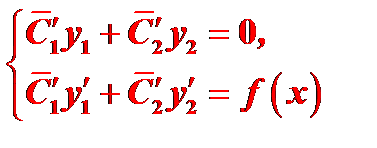 (5)
(5)
Так как определителем этой системы является определитель Вронского для линейно независимых решений 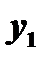 и
и 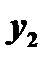 уравнения
уравнения 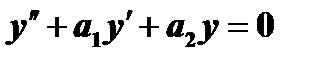 , то он не равен нулю; следовательно, решая систему, мы найдём
, то он не равен нулю; следовательно, решая систему, мы найдём 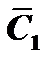 и
и 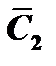 как определённые функции от
как определённые функции от 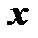 :
: 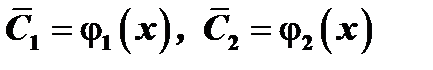 . Интегрируя, получим
. Интегрируя, получим 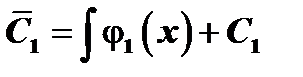 ,
, 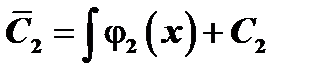 .
.
Подставив значения 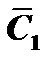 и
и 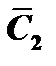 в выражение (1), найдём общее решение неоднородного уравнения.
в выражение (1), найдём общее решение неоднородного уравнения.
Решение 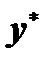 уравнения
уравнения 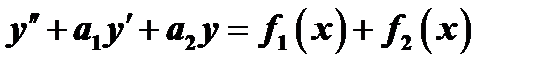 , где правая часть есть сумма двух функций
, где правая часть есть сумма двух функций 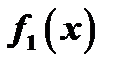 и
и 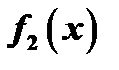 , можно представить в виде суммы
, можно представить в виде суммы 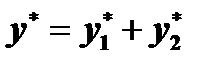 , где
, где 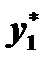 и
и 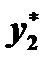 есть соответственно решения уравнений
есть соответственно решения уравнений
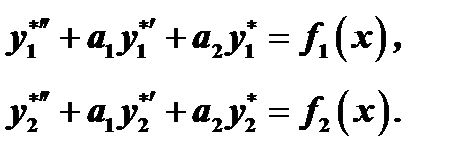
Дата добавления: 2015-12-29; просмотров: 566;
