Линейные однородные уравнения. Определения и общие свойства

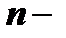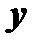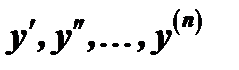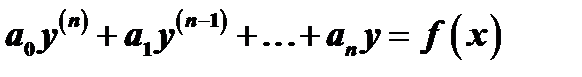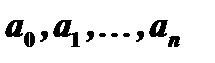Определение. Дифференциальное уравнение го порядка называется линейным, если оно первой степени относительно искомой функции и её производных и имеет вид , где и 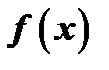- заданные функции от 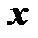или постоянные.

Если 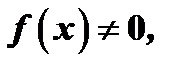то уравнение называется неоднородным, если же 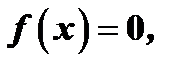то уравнение называется линейным однородным уравнением.

Определим некоторые основные свойства линейных однородных уравнений, ограничиваясь уравнениями второго порядка:

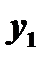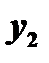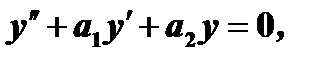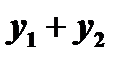1. Если и - два частных решения линейного однородного уравнения второго порядка то есть также решение этого уравнения.

2. Если 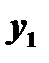есть решение уравнения 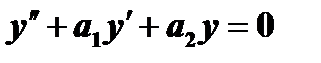и 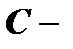постоянная, то 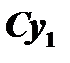есть также решение этого уравнения.

Определение. Два решения уравнения 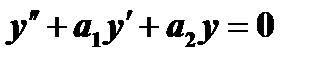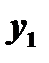и 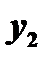называются линейно независимыми на отрезке 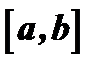, если их отношение на этом отрезке не является постоянным, т.е. если .

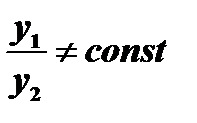Определение: Есл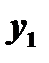и и 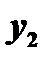функции от 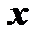, то определитель 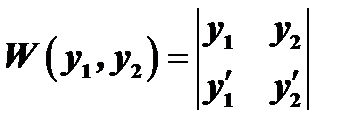называется определителем Вронского.

3. Если 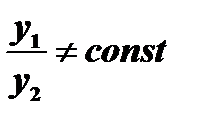, то .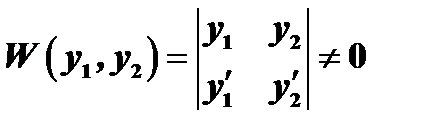

4. Есл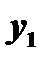и и 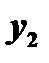- два линейно независимых решения уравнения 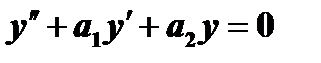, то 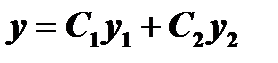есть его общее решение, где 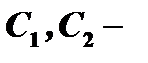произвольные постоянные.