Линейные уравнения первого порядка
Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной.
Линейное уравнение первого порядка имеет вид:
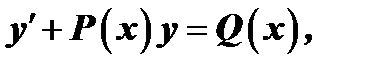 (1)
(1)
где 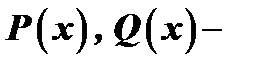 заданные непрерывные функции от
заданные непрерывные функции от 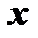 или постоянные числа.
или постоянные числа.
Решение линейного уравнения будем искать в виде произведения двух функции от 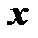 :
:
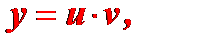 (2)
(2)
где 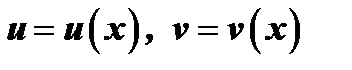 . Дифференцируя обе части последнего выражения, получим:
. Дифференцируя обе части последнего выражения, получим:
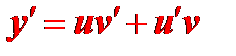 (3)
(3)
Значения 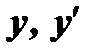 подставим в данное уравнение (1)
подставим в данное уравнение (1)
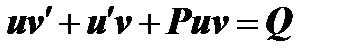
или 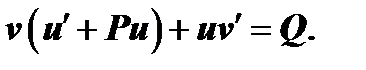
Выберем функцию 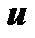 такой, чтобы
такой, чтобы
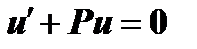 , (4)
, (4)
тогда 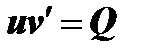 . (5)
. (5)
Решив сначала уравнение (4) и затем уравнение (5), найдём значения 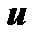 и
и 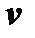 . Подставив значения
. Подставив значения 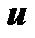 и
и 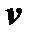 в (2) найдём решение уравнения (1).
в (2) найдём решение уравнения (1).
Замечание: Уравнение вида 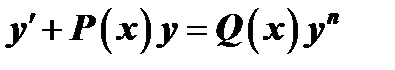 , (6)
, (6)
где 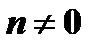 и
и 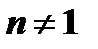 , называется уравнением Бернулли.
, называется уравнением Бернулли.
Уравнение Бернулли приводится к линейному следующим преобразованием: разделим все члены уравнения на 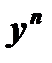
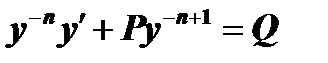 (7)
(7)
и произведём замену 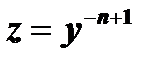 . (8)
. (8)
Тогда 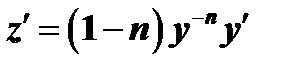 . (9)
. (9)
Подставив значения (8) и (9) в (7), получим 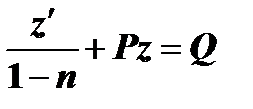 или
или
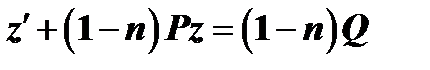 (10)
(10)
Решив линейное уравнение (10) и учитывая, что 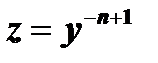 , найдём решение уравнения (6).
, найдём решение уравнения (6).
Заметим, что уравнение (6) часто можно решить как и линейное уравнение с помощью подстановки 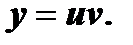
Дата добавления: 2015-12-29; просмотров: 583;
