Дифференциальные уравнения первого порядка
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Определения
Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную 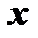 , искомую функцию
, искомую функцию 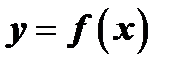 и её производные
и её производные 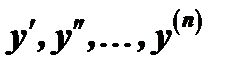 и записывается
и записывается 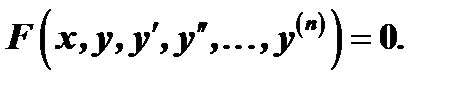
Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным. Если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например:
1) 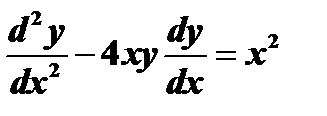 - обыкновенное дифференциальное уравнение 2-го порядка;
- обыкновенное дифференциальное уравнение 2-го порядка;
2) 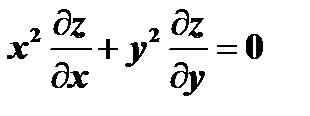 - уравнение в частных производных 1-го порядка.
- уравнение в частных производных 1-го порядка.
Определение 3. Решением дифференциального уравнения называется всякая функция 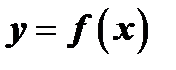 , которая, будучи подставлена в уравнение, превращает его в тождество.
, которая, будучи подставлена в уравнение, превращает его в тождество.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид 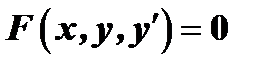 . Если это уравнение можно разрешить относительно
. Если это уравнение можно разрешить относительно 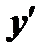 , то его можно записать в виде
, то его можно записать в виде 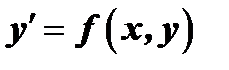 . Для такого уравнения справедлива теорема о существовании и единственности решения дифференциального уравнения:
. Для такого уравнения справедлива теорема о существовании и единственности решения дифференциального уравнения:
Т е о р е м а. Если в уравнении 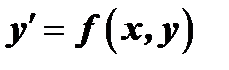 функция
функция 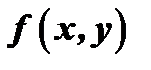 и её частная производная
и её частная производная 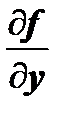 по
по 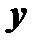 непрерывны в некоторой области
непрерывны в некоторой области 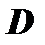 на плоскости
на плоскости 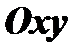 , содержащей некоторую точку
, содержащей некоторую точку 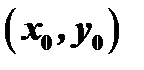 , то существует единственное решение этого уравнения
, то существует единственное решение этого уравнения 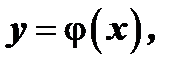 удовлетворяющее условию:
удовлетворяющее условию: 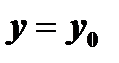 при
при 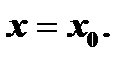
Условие, что 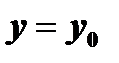 при
при 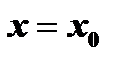 , называется начальным условием и записывается
, называется начальным условием и записывается 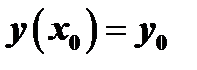 или
или 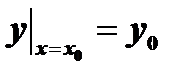 .
.
Общим решением дифференциального уравнения первого порядка называется функция 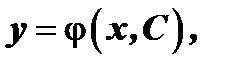 которая зависит от одного произвольного постоянного
которая зависит от одного произвольного постоянного 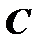 и удовлетворяет условиям:
и удовлетворяет условиям:
- она удовлетворяет дифференциальному уравнению при любом конкретном значении постоянного 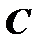 ;
;
- каково бы ни было начальное условие 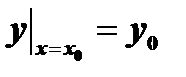 , можно найти такое значение
, можно найти такое значение 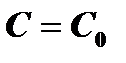 , что функция
, что функция 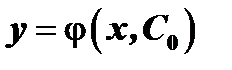 удовлетворяет данному начальному условию.
удовлетворяет данному начальному условию.
Частным решением называется любая функция 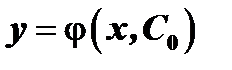 , которая получается из общего решения
, которая получается из общего решения 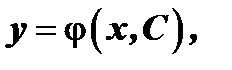 если в последнем произвольному постоянному
если в последнем произвольному постоянному 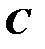 придать определённое значение
придать определённое значение 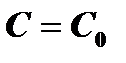 .
.
Дата добавления: 2015-12-29; просмотров: 579;
