Линейные однородные уравнения второго порядка с постоянными коэффициентами
Пусть дано однородное уравнение второго порядка
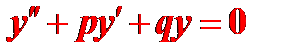 , (1)
, (1)
где 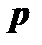 и
и 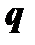 - постоянные числа.
- постоянные числа.
Согласно свойству (4) для определения общего решения уравнения надо найти два линейно независимых частных решения. Будем искать частные решения в виде
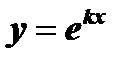 , где
, где  .
.
Тогда 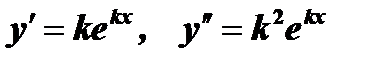 .
.
Подставим полученные выражения в данное уравнение
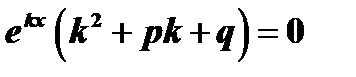 ,
,
откуда, т.к. 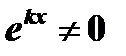 ,
, 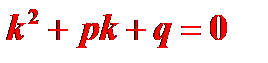 (2)
(2)
Уравнение (2) называется характеристическим уравнением уравнения (1). Решение уравнения (2) имеет вид:
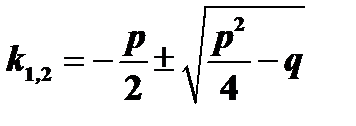
Возможны следующие случаи:
1. 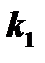 и
и 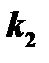 - действительные и притом не равные между собой;
- действительные и притом не равные между собой;
2. 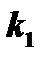 и
и 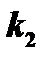 - действительные и притом равные между собой;
- действительные и притом равные между собой;
3. 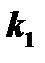 и
и 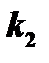 - комплексные числа.
- комплексные числа.
Рассмотрим каждый случай отдельно:
1. 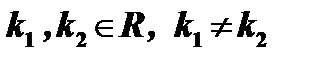
В этом случае 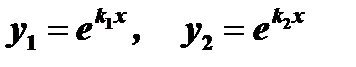 , причём
, причём 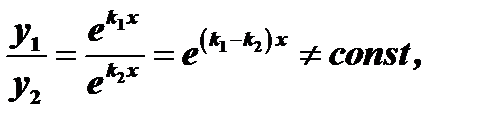 т.к.
т.к. 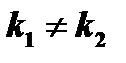 , следовательно, общее решение по свойству (4) имеет вид
, следовательно, общее решение по свойству (4) имеет вид
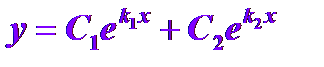
2. 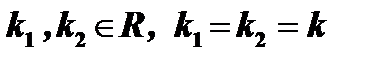
Одно частное решение можно искать в виде 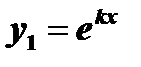 , но второе уже искать в таком же виде нельзя, т.к. они окажутся линейно зависимыми. Второе частное решение будем искать в виде
, но второе уже искать в таком же виде нельзя, т.к. они окажутся линейно зависимыми. Второе частное решение будем искать в виде 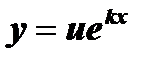 , где
, где 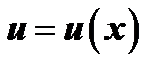 . Тогда
. Тогда 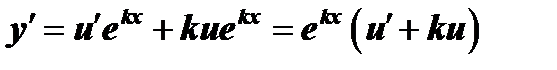 и
и 
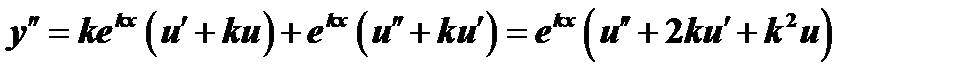 . Подставим значения
. Подставим значения 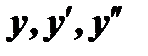 в уравнение (1):
в уравнение (1):
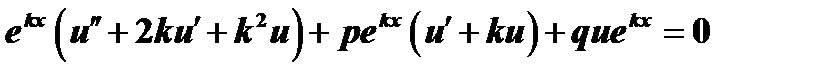
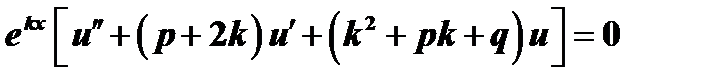 .
.
Т.к. 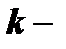 корень характеристического уравнения, то
корень характеристического уравнения, то 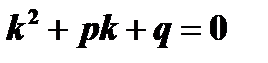 , кроме того
, кроме того 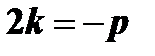 , т.к. корни равны между собой. Следовательно,
, т.к. корни равны между собой. Следовательно, 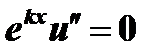 , откуда
, откуда 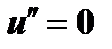 . Решая последнее уравнение получим
. Решая последнее уравнение получим 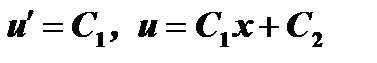 . Полагая
. Полагая 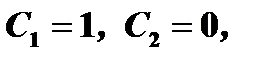 получим
получим 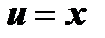 . Следовательно, второе частное решение можно искать в виде
. Следовательно, второе частное решение можно искать в виде 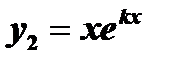 . Заметим, что
. Заметим, что 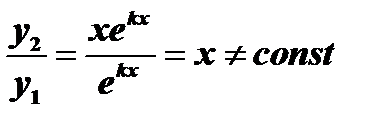 . По свойству (4) имеем
. По свойству (4) имеем 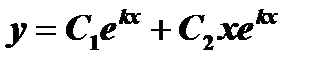 , т.е.
, т.е.
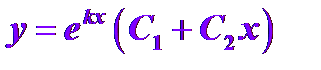
3. 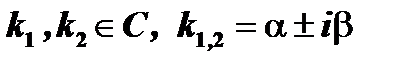
В этом случае 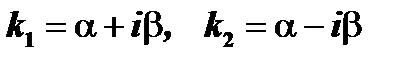 .
. 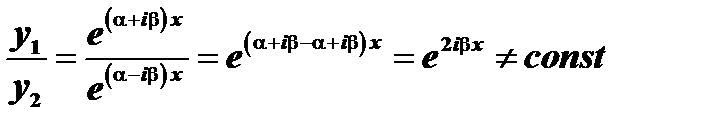 . Следовательно,
. Следовательно,
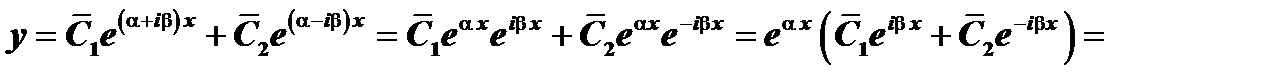
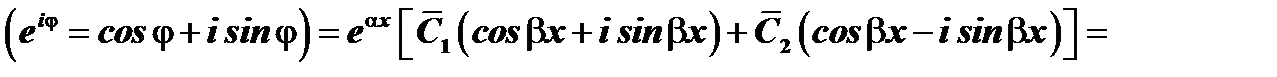
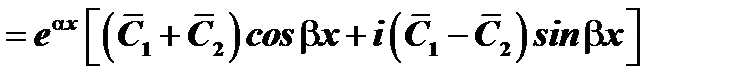 .
.
Обозначим 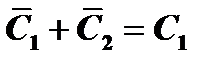 и
и 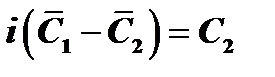 , тогда по свойству (4) общее решение:
, тогда по свойству (4) общее решение:
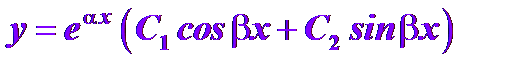
Дата добавления: 2015-12-29; просмотров: 638;
