Дифференциальные уравнения высших порядков
Дифференциальное уравнение  го порядка имеет вид:
го порядка имеет вид:
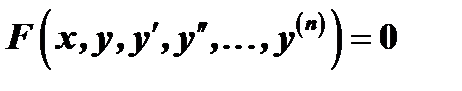
или, если его можно разрешить относительно 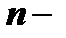 ой производной,
ой производной,

Для этих уравнений имеет место теорема о существовании и единственности решения:
Если в уравнении 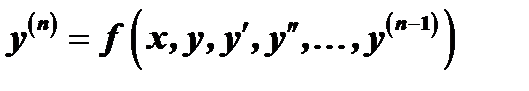 функция
функция  и её частные производные по аргументам
и её частные производные по аргументам 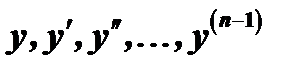 непрерывны в некоторой области, содержащей значения
непрерывны в некоторой области, содержащей значения 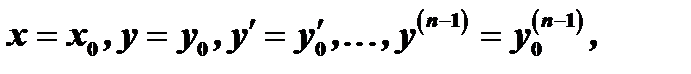 то существует и притом единственное решение
то существует и притом единственное решение  уравнения, удовлетворяющее условиям
уравнения, удовлетворяющее условиям
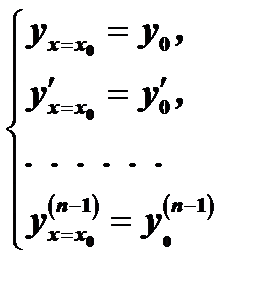
Эти условия называются начальными условиями.
Общим решением дифференциального уравнения 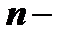 го порядка называется функция
го порядка называется функция 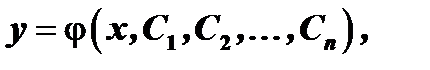 зависящая от
зависящая от  произвольных постоянных
произвольных постоянных 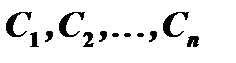 и такая, что:
и такая, что:
1) она удовлетворяет уравнению при любых значениях постоянных 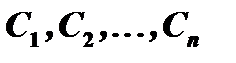 ;
;
2) при заданных начальных условиях

постоянные 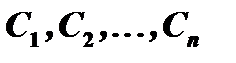 можно подобрать так, что функция
можно подобрать так, что функция  будет удовлетворять этим условиям.
будет удовлетворять этим условиям.
Всякая функция, получающаяся из общего решения при конкретных значениях постоянных 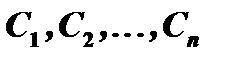 , называется частным решением.
, называется частным решением.
Уравнения вида 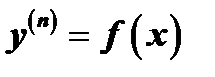
Простейшим уравнением 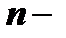 го порядка является уравнение вида
го порядка является уравнение вида 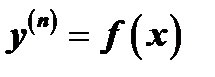 . Такие уравнения решаются путём интегрирования левой и правой части
. Такие уравнения решаются путём интегрирования левой и правой части 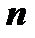 раз.
раз.
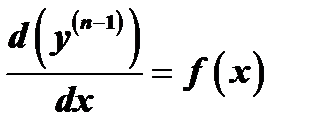
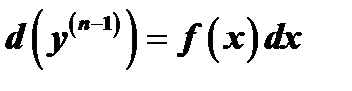
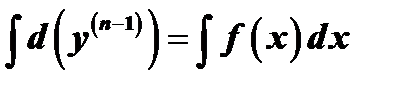

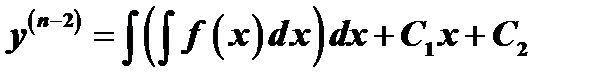
. . . . . . . . . . .
Дата добавления: 2015-12-29; просмотров: 697;
