Линейные однородные уравнения го порядка с постоянными коэффициентами

Рассмотрим линейное однородное уравнение 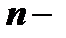го порядка:

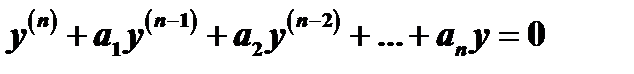
Для этого уравнения справедлива следующая теорема:

Если функции 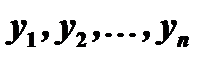являются линейно независимыми решениями данного уравнения, то его общее решение суть

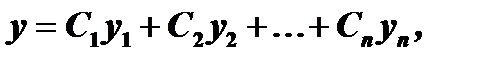
где 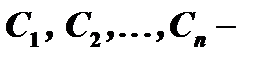произвольные постоянные.

Если коэффициенты данного уравнения постоянны, то общее решение находится так же, как и в случае уравнения второго порядка:

1. Составляем характеристическое уравнение

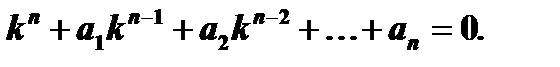
2. Находим корни характеристического уравнения

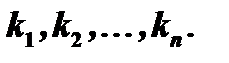
3. По характеру корней выписываем частные линейно независимые решения, руководствуясь тем, что:

3.1 каждому действительному однократному корню 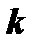соответствует частное решение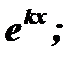

3.2 каждой паре комплексных сопряжённых однократных корней 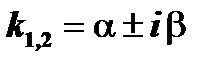соответствуют два частных решения 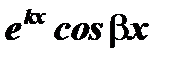и

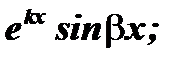
3.3 каждому действительному корню 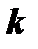кратности соответствует линейно независимых частных решений

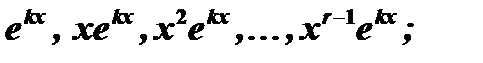
3.4 каждой паре комплексных сопряжённых корней 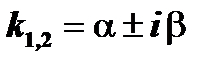кратности 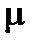соответствуют 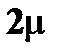частных решений

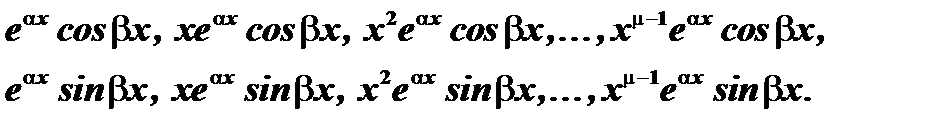
4. Найдя 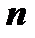линейно независимых частных решений 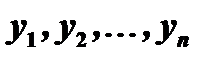, строим общее решение данного линейного уравнения

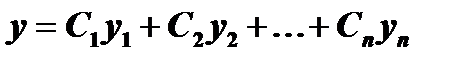
Описанные выше шаги можно объединить в таблицу:

Характер корня