Интегрирующий множитель
Пусть левая часть уравнения 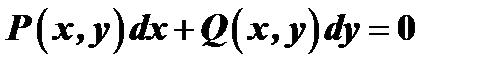 не есть полный дифференциал. Иногда удаётся подобрать такую функцию
не есть полный дифференциал. Иногда удаётся подобрать такую функцию 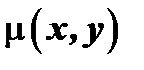 , после умножения на которую всех членов уравнения левая часть уравнения становится полным дифференциалом.
, после умножения на которую всех членов уравнения левая часть уравнения становится полным дифференциалом.
Общее решение полученного таким образом уравнения совпадает с общим решением первоначального уравнения; функция 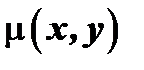 называется интегрирующим множителем данного уравнения.
называется интегрирующим множителем данного уравнения.
Для того чтобы найти 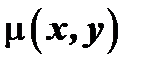 умножим обе части уравнении на неизыестный пока интегрирующий множитель
умножим обе части уравнении на неизыестный пока интегрирующий множитель 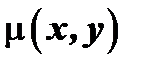 :
: 
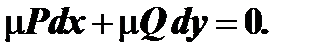
Для того чтобы последнее уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
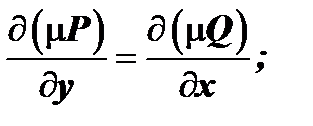
т.е. 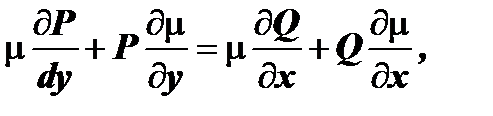 или
или 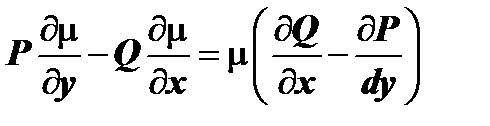 . После деления обеих частей последнего уравнения на
. После деления обеих частей последнего уравнения на 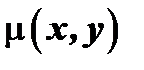 , получим:
, получим:
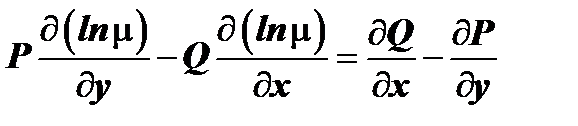 .
.
Задача нахождения 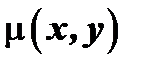 из последнего уравнения ещё труднее, чем первоначальная задача интегрирования данного уравнения. Только в некоторых частных случаях .
из последнего уравнения ещё труднее, чем первоначальная задача интегрирования данного уравнения. Только в некоторых частных случаях .
удаётся найти функцию 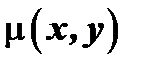
Пусть, например, данное уравнение допускает интегрирующий множитель, зависящий только от 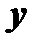 . Тогда
. Тогда
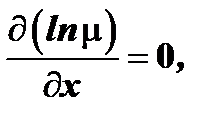
и для отыскания 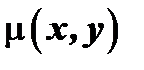 мы получаем обыкновенное дифференциальное уравнение
мы получаем обыкновенное дифференциальное уравнение
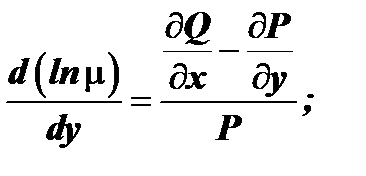
Откуда
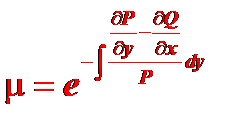
Аналогично, если у данного уравнения существует интегрирующий множитель, зависящий только от 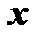 , то он находится по формуле
, то он находится по формуле
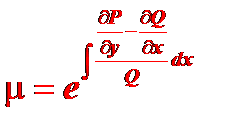
Дата добавления: 2015-12-29; просмотров: 1155;
