Однородные уравнения первого порядка
Прежде чем перейти к рассмотрению вопроса о решении однородных уравнений первого порядка познакомимся с понятием однородных функции.
Определение 1. Функция 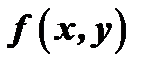 называется однородной функцией
называется однородной функцией 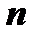 -го измерения относительно переменных
-го измерения относительно переменных 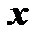 и
и 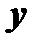 , если при любом
, если при любом 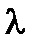 справедливо тождество
справедливо тождество
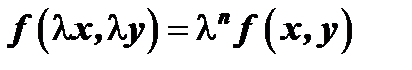 .
.
Так, например, функция 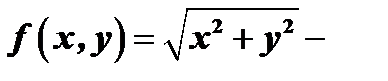 однородная функция первого измерения, т.к.
однородная функция первого измерения, т.к. 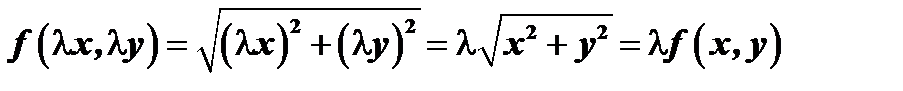 ;
;
функция 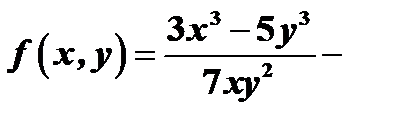 однородная функция нулевого измерения, т.к.
однородная функция нулевого измерения, т.к. 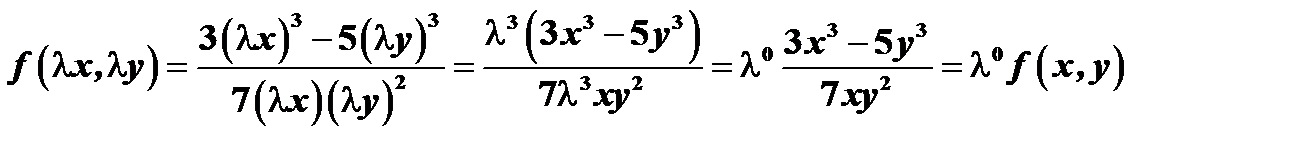 ;
;
функция 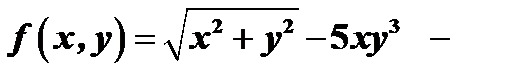 неоднородная функция, т.к.
неоднородная функция, т.к. 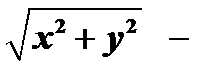 однородная функция первого измерения, а
однородная функция первого измерения, а 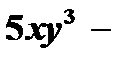 однородная функция четвёртого измерения.
однородная функция четвёртого измерения.
Определение 2. Уравнение первого порядка 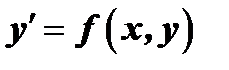 называется однородным относительно
называется однородным относительно 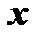 и
и 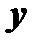 , если функция
, если функция 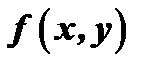 есть однородная функция нулевого измерения относительно
есть однородная функция нулевого измерения относительно 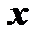 и
и 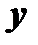 .
.
Однородные уравнения первого порядка приводятся к уравнениям с разделяющимися переменными с помощью подстановки
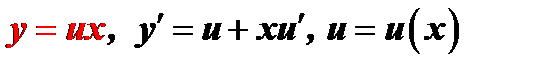
Уравнение вида 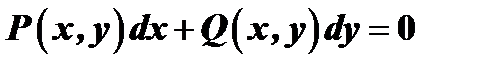 будет однородным тогда и только тогда, когда функции
будет однородным тогда и только тогда, когда функции 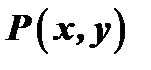 и
и 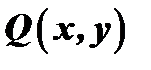 будут однородными функциями одного и того же измерения.
будут однородными функциями одного и того же измерения.
Например, 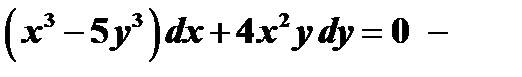 однородное уравнение;
однородное уравнение;
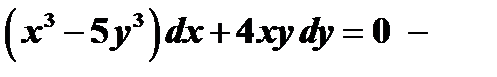 неоднородное уравнение.
неоднородное уравнение.
Замечание: Уравнения вида 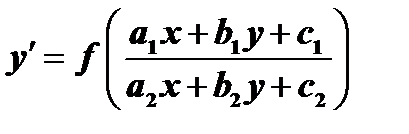 при
при 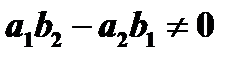 приводятся к однородным подстановкой
приводятся к однородным подстановкой 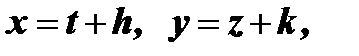 где
где 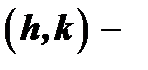 точка пересечения прямых
точка пересечения прямых 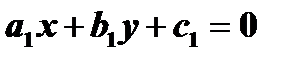 и
и 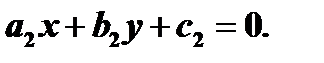 Таким образом, для определения
Таким образом, для определения 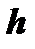 и
и 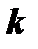 необходимо решить систему уравнений:
необходимо решить систему уравнений:
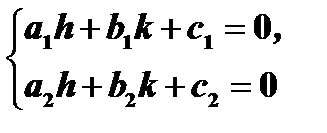
Если же 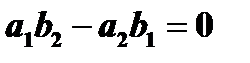 , то подстановка
, то подстановка 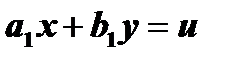 позволяет разделить переменные.
позволяет разделить переменные.
Дата добавления: 2015-12-29; просмотров: 703;
