Классификация событий
Теория вероятностей изучает модели экспериментов со случайными исходами, так называемых случайных экспериментов.
Определение. Случайным экспериментом (опытом или испытанием) называют осуществление комплекса условий или действий, при которых наблюдается соответствующее явление.
Рассматриваются только такие эксперименты, которые можно повторять при неизменном комплексе условий произвольное число раз (по крайней мере теоретически). При проведении случайного эксперимента объектом наблюдения может быть некоторый процесс, физическое явление или действующая система. Понятие «наблюдаемый результат» означает, что существует возможность зарегистрировать его с помощью того или иного прибора (в простейшем случае, визуально).
Любой наблюдаемый результат опыта называют исходом (случайным событием).
Событие может произойти, а может и не произойти в результате эксперимента.
Событие называется достоверным, если оно обязательно произойдет в этом опыте.
Событие называется невозможным, если оно в этом опыте произойти не может.
При математическом описании модели случайного эксперимента основным является понятие пространства элементарных исходов, связанного с данным опытом.
Определение. Пространством элементарных исходов 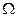 называют множество всех мыслимых взаимоисключающих исходов
называют множество всех мыслимых взаимоисключающих исходов 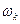 такое, что результатом эксперимента является один и только один исход. В математической модели пространство элементарных исходов – это произвольное множество, а его элементы – это сами элементарные исходы.
такое, что результатом эксперимента является один и только один исход. В математической модели пространство элементарных исходов – это произвольное множество, а его элементы – это сами элементарные исходы.
Определение.Подмножества множества 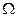 называют событиями и обозначают заглавными буквами
называют событиями и обозначают заглавными буквами 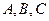 и т.п.
и т.п.
Говорят, что событие А произошло, если результатом эксперимента явился элементарный исход 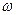 , принадлежащий А (
, принадлежащий А ( 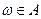 ).
).
Пустое множество 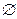 называют невозможным событием, а множество
называют невозможным событием, а множество 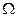 - достоверным событием.
- достоверным событием.
Примеры. 1.Эксперимент состоит в подбрасывании игральной кости один раз.
Результатом эксперимента является количество очков, выпавших на верхней грани. Элементарный исход 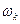 состоит в том, что
состоит в том, что 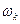 = {выпало к очков}. Пространство элементарных исходов
= {выпало к очков}. Пространство элементарных исходов 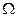 состоит из шести элементов:
состоит из шести элементов: 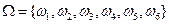 . Рассмотрим события:
. Рассмотрим события:
А={выпало 5 очков}, B={число выпавших очков четное}, C={выпало больше трех очков}, D={выпало дробное число очков}, F={выпало число, меньшее 7}.
Эти события рассматривают как подмножества множества 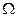 , а именно:
, а именно:
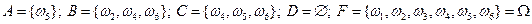 .
.
Отметим, что событие D – невозможное, а событие F – достоверное.
2.Рассмотрим следующий случайный эксперимент: матч по футболу между командами «Динамо» и «Спартак». Интересующие нас события: А={выиграла команда «Динамо»}, B={игра закончилась победой одной из команд}, C={игра закончилась со счетом 3:1 в пользу «Спартака»}, D={в игре забито не менее 3 голов}. Опишем пространство элементарных исходов и укажем подмножества, соответствующие указанным событиям. Что может служить исходом эксперимента, состоящего в проведении футбольного матча? Для полного и однозначного описания всех связанных с экспериментом событий, достаточно принять в качестве исхода счет матча. Запишем множество 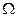 следующим образом:
следующим образом:
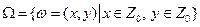 ,
,
где 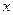 - количество голов, забитых командой «Динамо»,
- количество голов, забитых командой «Динамо», 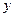 - количество голов, забитых командой «Спартак»,
- количество голов, забитых командой «Спартак», 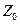 - множество неотрицательных целых чисел. Теоретически множество значений
- множество неотрицательных целых чисел. Теоретически множество значений 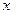 и
и 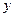 неограничено. Подмножества, соответствующие указанным событиям:
неограничено. Подмножества, соответствующие указанным событиям:
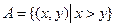 ,
, 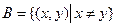 ,
, 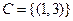 ,
, 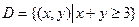 .
.
3.Эксперимент состоит в радиолокационном наблюдении воздушной цели. Наблюдаемый результат – положение светящегося пятна на экране индикатора цели, имеющего форму круга, радиуса 10 см. Опишем пространство элементарных исходов и следующие события: A={цель находится в первом квадранте}, B={цель находится в круге радиуса 5 см с центром в центре экрана}. Все интересующие нас события связаны с регистрацией положения светящегося пятна на экране. Удобной формой математического описания элементарного исхода являются координаты точки на плоскости в декартовой системе координат, связанной с центром экрана. Таким образом, пространство элементарных исходов бесконечно, непрерывно и может быть записано в виде:
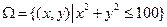 .
.
Подмножества, соответствующие указанным событиям:
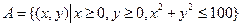 ,
, 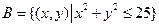 .
.
Дата добавления: 2016-01-09; просмотров: 1276;
