Независимость событий
Определение.Вероятность события 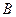 при условии, что событие A произошло, называется условной вероятностью события
при условии, что событие A произошло, называется условной вероятностью события 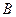 и обозначается:
и обозначается: 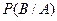 или
или 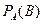 .
.
Условные вероятности определяются формулами:
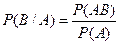 ,
, 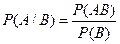 , где
, где 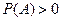 ,
, 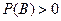 .
.
Определение.События А и В называются независимыми, если условная вероятность события А, при условии, что событие В произошло, равна безусловной вероятности этого события: 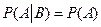 . Аналогично,
. Аналогично, 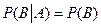 .
.
Теорема 1 (Теорема умножения вероятностей).Вероятность произведения двух событий равна произведению вероятности одного их них на условную вероятность другого при условии, что первое событие произошло:
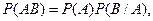
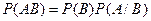 .
.
Следствие. Вероятность произведения двух независимых событий равна произведению их вероятностей: 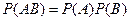 .
.
Это утверждение иногда принимают за определение независимых событий.
Теорема 2.Вероятность произведения 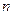 событий равна произведению вероятности одного их них на условные вероятности всех остальных в предположении, что все предыдущие события наступили:
событий равна произведению вероятности одного их них на условные вероятности всех остальных в предположении, что все предыдущие события наступили:
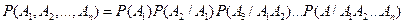 .
.
В частности, для трех событий 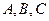 эта формула имеет вид
эта формула имеет вид 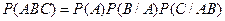 .
.
Определение.События 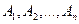 называются независимыми в совокупности (или просто независимыми), если каждое из них и произведение любого числа
называются независимыми в совокупности (или просто независимыми), если каждое из них и произведение любого числа 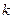 остальных
остальных 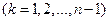 являются независимыми.
являются независимыми.
Замечание.Из попарной независимости событий не следует их независимость в совокупности.
Если события 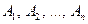 независимы в совокупности, то
независимы в совокупности, то
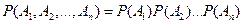 .
.
Теорема 3.Если событие 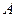 состоит в появлении хотя бы одного из независимых событий
состоит в появлении хотя бы одного из независимых событий 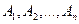 , то
, то 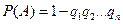 , где
, где 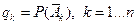 ; (
; ( 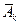 - событие, противоположное событию
- событие, противоположное событию 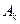 ).
).
Если все независимые события 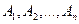 имеют одну и ту же вероятность
имеют одну и ту же вероятность 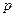 , то вероятность появления хотя бы одного из них определяется формулой:
, то вероятность появления хотя бы одного из них определяется формулой: 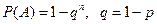 .
.
Пример.В урне имеется 6 красных, 8 синих, 4 белых шара. Каждое испытание состоит в том, что из урны берут наудачу один шар и не возвращают обратно. Найти вероятность того, что в первом испытании будет извлечен красный шар, при втором – синий, при третьем – белый.
Решение. Эксперимент состоит в последовательном извлечении без возвращения трех шаров из 18. Рассмотрим события:
событие 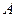 - {извлекли красный шар};
- {извлекли красный шар};
событие 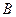 - {извлекли синий шар};
- {извлекли синий шар};
событие 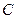 - {извлекли белый шар}.
- {извлекли белый шар}.
Нас интересует событие, состоящее в одновременном появлении всех этих событий, т.е. произведение АВС. По теореме умножения вероятностей для трех событий: 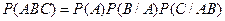 , надо найти следующие вероятности:
, надо найти следующие вероятности:
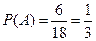 (вероятность вытащить красный шар),
(вероятность вытащить красный шар), 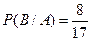 (вероятность вытащить синий шар, при условии, что один красный шар уже изъят),
(вероятность вытащить синий шар, при условии, что один красный шар уже изъят), 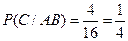 (вероятность извлечь белый шар, при условии, что уже извлекли и красный шар, и синий). Тогда окончательно получаем:
(вероятность извлечь белый шар, при условии, что уже извлекли и красный шар, и синий). Тогда окончательно получаем: 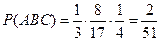 .
.
Пример.В каждом из трех ящиков имеется по 24 детали; при этом в первом ящике 18, во втором 20, в третьем 22 стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три извлеченные детали будут стандартными.
Решение.Эксперимент состоит в извлечении трех любых деталей из разных ящиков. Рассмотрим следующие события:
событие 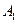 - { из первого ящика извлекли стандартную деталь },
- { из первого ящика извлекли стандартную деталь },
событие 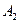 - { из второго ящика извлекли стандартную деталь },
- { из второго ящика извлекли стандартную деталь },
событие 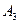 - { из третьего ящика извлекли стандартную деталь }.
- { из третьего ящика извлекли стандартную деталь }.
Нас интересует событие, состоящее в том, что рассмотренные 3 события произошли одновременно, т.е. произведение 3 событий: А1 А2 А3. Все эти события независимы в совокупности, т.к. извлечение из одного ящика стандартной детали никак не влияет на то, какая деталь будет извлечена из другого ящика. Поэтому, используем следующую формулу умножения вероятностей: 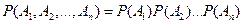 . Вероятности указанных событий:
. Вероятности указанных событий:
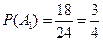 ,
, 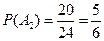 ,
, 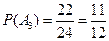 . Окончательно получаем
. Окончательно получаем 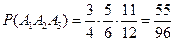 .
.
Пример. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0.9; вторым – 0.8; третьим – 0.7. Найти вероятность того, что а) только один из стрелков попадет в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
Решение.Эксперимент состоит в проведении 3 выстрелов тремя стрелками. Рассмотрим следующие события:
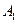 - { первый стрелок поразил цель },
- { первый стрелок поразил цель },
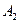 - {второй стрелок поразил цель },
- {второй стрелок поразил цель },
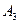 - {третий стрелок поразил цель }.
- {третий стрелок поразил цель }.
Так как каждый стреляет независимо от другого, эти события независимы в совокупности.
Пусть 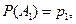
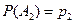 ,
, 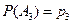 , тогда
, тогда 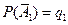 ,
, 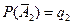 ,
, 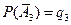 . Введем в рассмотрение вспомагательные события:
. Введем в рассмотрение вспомагательные события:
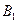 - { в цель попал только первый стрелок},
- { в цель попал только первый стрелок},
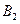 - { в цель попал только второй стрелок},
- { в цель попал только второй стрелок},
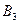 - { в цель попал только третьим стрелок}.
- { в цель попал только третьим стрелок}.
Опишем эти события через А1, А2, А3. Имеем: 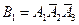 (первый попал, а второй и третий не попали),
(первый попал, а второй и третий не попали), 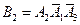 ,
, 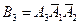 .
.
Пусть А – {в цель попал только один стрелок}, тогда А=В1+В2+В3 (попал только первый или только второй, или только третий). События 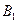 ,
, 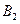 ,
, 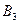 несовместны, т.к. не могут произойти одновременно. Тогда
несовместны, т.к. не могут произойти одновременно. Тогда 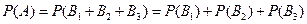 . Так как
. Так как 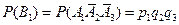 ,
, 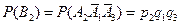 ,
, 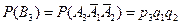 ,
,
то 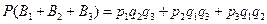 .
.
Пусть 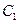 - { в цель попали только второй и третий стрелки};
- { в цель попали только второй и третий стрелки};
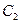 - { в цель попали только первый и третий стрелки};
- { в цель попали только первый и третий стрелки};
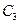 - { в цель попали только первый и второй стрелки}.
- { в цель попали только первый и второй стрелки}.
Тогда 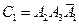 ,
, 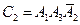 ,
, 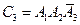 , причем эти события несовместны. Если В - {в цель попали только два стрелка}, то
, причем эти события несовместны. Если В - {в цель попали только два стрелка}, то 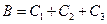 и
и
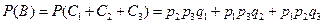 .
.
Пусть С - {в цель попали все три стрелка}, тогда 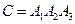 и
и 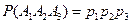 .
.
По условию задачи 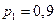 ,
, 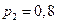 ,
, 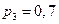 . Следовательно,
. Следовательно, 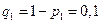 ,
, 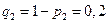 ,
, 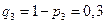 . Подставляя эти значения в полученные формулы, окончательно получаем:
. Подставляя эти значения в полученные формулы, окончательно получаем:
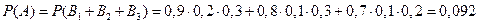 ;
; 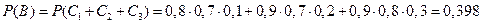 ;
; 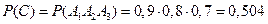 .
.
Дата добавления: 2016-01-09; просмотров: 1015;
