Последовательность независимых испытаний. Формула Бернулли
Пусть производится серия из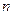 
независимых опытов, в каждом из которых может произойти некоторое событие 
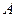. Вероятность того, что это событие произойдет в одном опыте, равна p и называется вероятностью успеха. Вероятность того, что 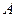не произойдет в данном опыте, равна 
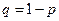. Будем считать, что вероятность успеха не изменяется от опыта к опыту, не зависит от исходов предыдущих опытов и не влияет на исходы последующих опытов.
Теорема 6. Вероятность того, что в серии из 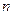независимых испытаний событие 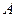появится ровно 
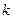раз (и не появится 
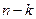раз), равна
,
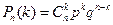где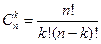 
, 
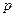- вероятность появления события 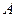в каждом испытании, 
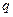- вероятность события 
( ).
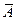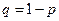Эту формулу называют формулой Бернулли.
Пример. Для стрелка, выполняющего упражнение в тире, вероятность попасть в «яблочко» при одном выстреле не зависит от результатов предшествующих выстрелов и равна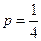 
. Спортсмен сделал 5 выстрелов. Найти вероятность событий: А – {спортсмен попал ровно 2 раза}, B – {спортсмен попал не меньше 4 раз}.
Решение. Производится серия из 5 выстрелов. При каждом выстреле спортсмен попадает с вероятностью 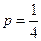и «мажет» с вероятностью 
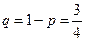. Используя формулу Бернулли, находим вероятность события А: 
.
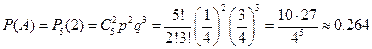Событие В есть сумма несовместных событий: {произошло равно 4 попадания} или {произошло равно 5 попаданий}. Поэтому получаем:
.
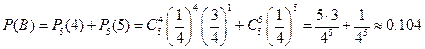Дата добавления: 2016-01-09; просмотров: 1163;