Формула полной вероятности. Формула Байеса
Определение.Говорят, что события 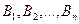 образуют полную группу событий, если они попарно несовместны, т.е.
образуют полную группу событий, если они попарно несовместны, т.е. 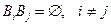 и
и 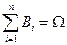 .
.
Пусть событие А может произойти одновременно с одним из несовместных событий 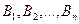 , образующих полную группу. Эти события принято называть гипотезами.
, образующих полную группу. Эти события принято называть гипотезами.
Теорема 4 (Теорема полной вероятности).Вероятность события А, которое может наступить лишь при условии появления одной из гипотез 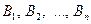 , равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
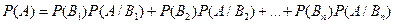 .
.
Формула 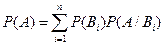 - называется формулой полной вероятности.
- называется формулой полной вероятности.
Вероятность гипотезы 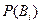 до проведения эксперимента называют априорной. Если известен результат эксперимента, то можно переоценить вероятность гипотезы
до проведения эксперимента называют априорной. Если известен результат эксперимента, то можно переоценить вероятность гипотезы
Теорема 5 (Теорема Байеса). Вероятность гипотезы после того, как известно, что в результате опыта события А произошло, дается формулой: 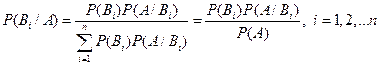 .
.
Эту формулу называют формулой Байеса.
Пример.Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0.8, а второго – 0.9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.
Решение. Рассмотрим следующие события:
А - {извлекли стандартную деталь},
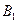 - {деталь извлечена из первого набора},
- {деталь извлечена из первого набора},
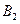 - { деталь извлечена из второго набора}.
- { деталь извлечена из второго набора}.
События В1 и В2 независимы и исчерпывают все возможные исходы эксперимента, т.е. 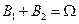 . Поскольку выбирается любой из двух наборов, то эти события равновероятны, т.е.
. Поскольку выбирается любой из двух наборов, то эти события равновероятны, т.е. 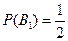 и
и 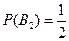 .
.
Вероятность того, что стандартная деталь будет извлечена из первого набора: 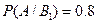 .
.
Вероятность того, что стандартная деталь будет извлечена из второго набора: 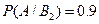 .
.
Искомая вероятность события А, т.е. того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна:
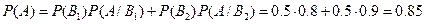 .
.
Пример.Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0.6, а ко второму – 0.4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0.94, а вторым – 0.98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Рассмотрим следующие события:
событие А – { деталь признана стандартной},
событие 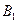 - {деталь проверил первый контролер},
- {деталь проверил первый контролер},
событие 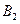 - {деталь проверил второй контролер}.
- {деталь проверил второй контролер}.
Требуется найти вероятность того, что произошло событие 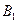 при условии, что деталь признана стандартной. Будем использовать формулу Байеса:
при условии, что деталь признана стандартной. Будем использовать формулу Байеса: 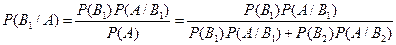 .
.
По условию задачи имеем:
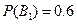 {вероятность того, что деталь попадет к первому контролеру};
{вероятность того, что деталь попадет к первому контролеру};
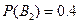 {вероятность того, что деталь попадет ко второму контролеру};
{вероятность того, что деталь попадет ко второму контролеру};
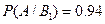 {вероятность того, что годная деталь будет признана первым контролером стандартной};
{вероятность того, что годная деталь будет признана первым контролером стандартной};
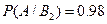 {вероятность того, что годная деталь будет признана вторым контролером стандартной}.
{вероятность того, что годная деталь будет признана вторым контролером стандартной}.
Искомая вероятность 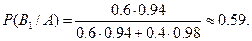
Дата добавления: 2016-01-09; просмотров: 1296;
