Дискретные случайные величины

Для исследования различных явлений, встречающихся в природе, технике, социологии и др. бывает недостаточно только понятия случайного события. На протяжении столетия формировалось еще одно понятие – понятие случайной величины. Случайная величина – это переменная величина, принимающая в зависимости от случая те или иные значения, но заранее, до опыта неизвестно, какие именно.

Примеры. 1. В течении дня на телефонную станцию поступают вызовы. Тогда количество вызовов в данный конкретный день есть случайная величина, возможные значения которой, теоретически, от нуля до бесконечности.

2.Спортсмен делает пять выстрелов по мишени. Количество попаданий в «яблочко» - есть случайная величина, возможные значения которой от нуля до пяти, причем до эксперимента неизвестно, сколько раз спортсмен поразит цель.

3.Диаметр изготовленной детали теоретически должен быть равен а. Однако на практике этот диаметр отличается от теоретического значения. Погрешность изготовления детали есть величина случайная, возможные значения которой принадлежат промежутку 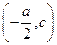, который связан с реальными условиями производства.

Рассмотрим вероятностное пространство 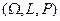, связанное с некоторым экспериментом.

Определение. Случайной величиной называется действительная числовая функция 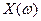, определенная для 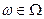, такая, что при всех действительных значениях 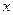множество 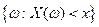принадлежит алгебре событий .

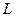Случайные величины принято обозначать большими буквами латинского алфавита: X, Y, Z, а их значения – малыми: x, y, z.

Определение.Случайная величина называется дискретной (ДСВ), если множество ее значений конечное или счетное. Случайная величина называется непрерывной (НСВ), если множество значений сплошь заполняет отрезок числовой оси или всю числовую ось.

В примерах 1 и 2 рассмотрены дискретные случайные величины, в примере 3 – непрерывная.

Чтобы задать случайную величину, недостаточно знать только ее возможные значения. Необходимо также установить вероятность того, что случайная величина примет то, или иное значение.

Определение.Законом распределения случайной величины 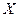называется соотношение между ее значениями 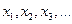и их вероятностями 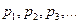; здесь 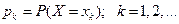(вероятность того, что случайная величина 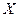примет значение ).

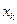Закон распределениядискретной случайной величины 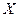, принимающей конечное множество значений 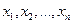с вероятностями 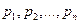, соответственно, можно задать таблицей

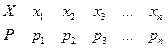
или формулами ; .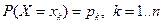

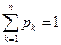Закон распределениядискретной случайной величины 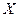, принимающей бесконечную последовательность значений 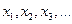с вероятностями 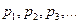соответственно, задается соотношениями:

; .

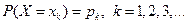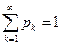Если значения упорядочены по возрастанию, то такую таблицу называют рядом распределения.

Еще один способ задать закон распределения – определить функцию распределения случайной величины.