В 4-ичную последовательность
Согласование модуляции и кодирования
Реализуемые значения вероятности ошибочного приёма символов передаваемого сообщения при заданной полосе частот DF и скорости передачи информации В или достижимые значения удельной скорости передачи информации при заданной вероятности ошибочного приёма зависят как от способа кодирования, так и от вида используемых сигналов (способа модуляции).
Предельные возможности системы передачи информации можно оценить с помощью выражения (по Шеннону) для пропускной способности С гауссовского непрерывного канала связи с полосой частот DF:
C = DF log2(1+ 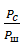 ) .
) .
В этом выражении Рс = ЕбВ — средняя мощность сигнала, где Еб — энергия, затрачиваемая на передачу одного бита информации; В =1/Тб— скорость передачи информации источника; Тб— время передачи источником одного бита информации; РшN0DF — средняя мощность шума в полосе частот DF; N0/2 — спектральная плотность мощности шума. Из предыдущего выражения следует, что реальная скорость передачи информации В, которая меньше С, удовлетворяет неравенству
B £ DF×log2[1+(Еб×В)/(DF×N0)] или Еб/В ³ (2b-1)/b ,
где b=B/DF (бит×с-1/Гц) – удельная скорость передачи информации.
Рис. 7.3. Зависимость удельной скорости передачи от энергетических затрат на один бит
Как известно, вероятность ошибочного приёма в конкретной системе определяется отношением Еб/N0. Предыдущее неравенство показывает, что возрастание удельной скорости передачи требует увеличение энергетических затрат(Еб) на один бит, что иллюстрирует рис. 7.3.
Любая система связи может быть описана точкой, лежащей ниже приведённой на рис. 7.3 кривой (область б), и для любой точки можно создать систему связи, у которой вероятность ошибочного приёма может быть сделана настолько малой, насколько это желательно. История развития систем связи в какой-то степени представляет собой серию попыток приблизить их к этой предельной кривой, сохраняя низкую вероятность ошибочного приема бита. Такие системы используют как модемную технику, так и технику кодирования.
С помощью модемной техники стремятся к такому расположению точек в сигнальном пространстве, при котором обеспечивается высокая удельная скорость (сигналы расположены достаточно плотно) и одновременно высокая помехоустойчивость (сигналы находятся достаточно далеко друг от друга). Помехоустойчивое кодирование позволяет снизить необходимую величину Еб, поскольку расстояние между кодовыми комбинациями увеличивается.
При многопозиционной модуляции, когда сигналом «переносится» блок из n кодовых символов, также важно правильно выбрать манипуляционный код, определяющий правило сопоставления с каждым передаваемым сигналом определённого блока кодовых символов. Общий принцип сопоставления известен: большему расстоянию по Хэммингу между кодовыми блоками должно соответствовать большее расстояние по Евклиду между отображающими их сигналами. Этому требованию в первом приближении удовлетворяет код Грея.
Следующим шагом в повышении эффективности систем является согласование всех вышеуказанных этапов формирования сигнала (формирование кодовых комбинаций и сигналов, а также их сопоставление). Комбинирование различных ансамблей сигналов, помехоустойчивых кодов и манипуляционных кодов порождает множество вариантов построения таких систем. На практике (при простой реализации) проблема создания пары кодек-модем(кодем) достаточно успешно решается для каналов с ограниченной полосой пропускания. В них обеспечение заданной скорости передачи информации (и удельной скорости) связано с переходом к многопозиционной модуляции. Но при этом требуется увеличение Еб, которое может быть скомпенсировано применением помехоустойчивого кодирования в обмен на снижение удельной скорости передачи b. Необходимо так подобрать семейство сигналов и код, чтобы получить энергетический выигрыш от кодирования (ЭВК) без расширения занимаемой полосы частот. Что это возможно, вытекает из следующего рассуждения.
Рис. 7.4,а. Согласование модулятора и кодера для случая ФМ-8-НСК(2/3)
Предположим, в системе без кодирования используется 2n-1-ичная модуляция. При этом каждый элемент сигнала отображает (n-1) бит. Расширим множество сигналов до 2n и применим код (n, n-1). Поскольку скорость передачи элементов сигналы не изменилась, то система с кодированием будет занимать такую же полосу частот, как и система без кодирования, и каждому элементу сигнала будет соответствовать то же число (n-1) информационных бит. Если код выбран удачно, то кодирование позволяет уменьшить требуемое значение Еб на величину, равную выигрышу от кодирования.
В качестве примера (рис. 7.4) рассмотрим согласование модулятора и кодера для случая ФМ-8-НСК(2/3). Схема кодера представлена на рис. 7.4,а. Для сравнения информационная последовательность также передаётся сигналом ФМ-4. Эта информационная последовательность двоичных символов U разбивается на два потока u1 и u2, и на выходе кодера в каждом такте образуется комбинация из кодовых символов а1, а2, а3. В модуляторе ФМ-8 используется код Грея.
Соответствие кодовых трибитов сигналам на выходе модулятора определяется (рис. 7.4,б) соотношениями:
| Рис. 7.4,б,в. Согласование модулятора и кодера для случая ФМ-8-НСК(2/3)
|
d0 = 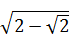 = 0.765 , d1 =
= 0.765 , d1 = 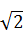 = 1.414 ,
= 1.414 ,
d2 = 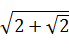 = 1.848 , d3 = 2 .
= 1.848 , d3 = 2 .
Сравнительный анализ системы ФМ-8-НСК(2/3) с декодированием по алгоритму Витерби и основной системы ФМ-4 без кодирования (ей отвечают 4 точки на координатных осях рис. 7.4,б) обнаруживает небольшой ЭВК(порядка 1,1 дБ) для первой системы. Значение ЭВК может быть увеличено (до 3 дБ), если применить более рациональное кодирование (рис. 7.4,в).
Здесь первые два символа, соответствующие каждой сигнальной точке (подчёркнуты), задаются кодером (рис. 7.5) НСК(1/2). Третий символ представляет собой незакодированный символ исходной информационной последовательности. Таким образом, и в этом случае в каждом элементе сигнала отображается два информационных символа. При указанном отображении максимально разделены пары сигнальных точек, в которых закодированные дибиты совпадают, а незакодированные различны. Во многих случаях оказывается наиболее эффективным применять кодирование лишь к некоторым информационным битам кодового блока. При значительном различии расстояний между сигналами информацию можно передавать без всякого кодирования.
Сигнально-кодовые конструкции Унгербоека
| Рис. 7.5. Структурная схема
свёрточного несистематического
кодирования (1/2)
|
В начале 80-х годов австриец Готфрид Унгербоек (Gottfried Ungerboeck,сотрудник IBM Zurich Research Laboratory) опубликовал статью, в которой, анализируя СКК на базе ансамбля сигналов ФМ-8 и свёрточного кода с R = k/(k+1), сформулировал ряд правил построения СКК. Ввиду сказанного, СКК подобного вида (trellis-coded modulation — TCM) часто называют СКК Унгербоека.
Общая схема передачи дискретных сообщений с использованием СКК представлена на рис. 7.6. По способу согласования модуляции и кодирования СКК Унгербоека относятся к конструкциям, полученным на основе разбиения ансамбля сигналов на вложенные подансамбли. Разбиение для ансамбля сигналов ФМ-8 представлено на рис. 7.7. Расстояния между сигнальными точками показаны на рис. 7.4,б.
Рис.7.6. Общая схема передачи с использованием СКК
Как следует из рис. 7.7, исходный ансамбль разбивается на подансамбли при максимальном увеличении наименьших евклидовых расстояний demin между сигналами внутри под ансамблей d0< d1 < d2< d3. Разбиение осуществляется поэтапно. В данном примере таких этапов три, которые заключаются в разбиении каждого из подансамблей предыдущего этапа на два равноэлементных подансамбля.
Рис. 7.7. Разбиение ансамбля сигналов на вложенные подансамбли и построение МК
Разбиение ансамбля сигналов на вложенные подансамбли (рис. 7.7) Унгербоек сопровождает определённым алгоритмом построения МК. Достижение наибольшей помехоустойчивости напрямую связано с увеличением евклидова расстояния между передаваемыми сигнальными последовательностями. Решётчатая диаграмма (РД) свёрточного кода, рёбра которой промаркированы сигнальными точками, полностью отображает весь набор разрешённых сигнальных последовательностей. Минимальное евклидово расстояние между несовпадающими канальными последовательностями называется свободным евклидовым расстоянием def. Эти последовательности расходятся из одного из одного и того же состояния и сходятся в одном и том же состоянии РД. Свободное евклидово расстояние характеризует предельную помехоустойчивость.
Таким образом, величина свободного евклидова расстояния def зависит от маркировки рёбер РД сигнальными точками (канальными символами). Унгербоек на примере ансамбля сигналов ФМ-8 (рис.7.7) сформулировал четыре необходимых правила маркировки рёбер РД сигнальными точками:
§ все сигнальные точки используемого ансамбля сигналов должны встречаться с одинаковой частотой и с определённой степенью регулярности и симметричности;
§ переходы из одного и того же состояния соответствуют сигналам из подансамблей В0 или В1;
§ переходы в одно и то же состояние соответствуют сигналам из подансамблей В0 или В1;
§ параллельные переходы между состояниями соответствуют сигналам из подансамблей С0, или С1, или С2, или С3.
| Рис. 7.8. ССК (n = 3, R = 2/3) с обратной связью для СКК Унгербоека (ФМ-8)
|
Четыре правила Унгербоека не определяют достаточные условия построения СКК с максимальным свободным евклидовым расстоянием def . Конкретные СКК находились путём перебора схем кодеров по критерию максимума def при заданных МК, соответствующих описанному алгоритму разбиения. Заметим, что при этом МК для ансамблей ФМ-М соответствуют натуральному двоичному коду. В частности, Унгербоек произвёл перебор по систематическим с обратными связями схемам свёрточных кодов для различных ансамблей сигналов с М = 8…64. На рис. 7.8 приведена найденная Унгербоеком схема систематического с обратной связью кодера СКК (n = 3, R = 2/3). В качестве сигнального ансамбля используется ФМ-8 с натуральным двоичным МК (рис. 7.7).
Сигнально-кодовые конструкции «последней мили»
Проблема удаленного высокоскоростного доступа к сетям передачи данных общего пользования на основе медно-кабельных линий привязки активно решается многими телекоммуникационными компаниями: идет поиск способов и технических решений для ограничения спектра передаваемых сигналов, спектральной совместимости различных систем передачи и повышения помехозащищенности передаваемой информации. Этот способ удалённого доступа в англоязычной литературе получил название xDSL (DSL — Digital Subscriber Loop), имеющий несколько разновидностей: HDSL (High-bit-rate DSL), SDSL (Single Pair Symmetrical DSL), ADSL (Asymmetric DSL), VDSL (Very High-bit-rate DSL).
| Многожильный
медный кабель
(сечение)
|
| Медные
проводники
в полиэтиленовой
изоляции
|
| Зона
паразитного
излучения
|
| Многожильный
медный
кабель
|
Рис. 7.9. Медно-кабельная линия привязки и «модемы последней мили»
С теоретической точки зрения проблема реализации высокоскоростного удалённого доступа на основе медно-кабельных линий привязки (так называемая проблема «последней мили») сводится к известной задаче (в области электросвязи): передача дискретных сообщений по каналам с ограниченной полосой пропускания. Другими словами, как передать с высокой скоростью дискретное сообщение (с заданной вероятностью ошибки) по кабельной линии связи, имеющей ограниченную полосу пропускания и подвергающей передаваемые сигналы сильным нелинейным искажениям, вызванным электромагнитным излучением (наводками) от других близко лежащих проводов (рис. 7.9).
Ситуация с использованием многопарных медных кабелей усугубляется еще и тем, что практически невозможно априори спрогнозировать (смоделировать) помеховую обстановку внутри конкретного кабеля ввиду следующих причин:
1. каждый кабель уникален и обладает своим «рисунком паразитного излучения» из-за своих конструктивных особенностей (дефектов производства и т.п.);
2. характер залегания и прокладки кабеля (наличие изгибов, перекручивания и т.п.);
3. наличие вдоль трассы прокладки кабеля мощных источников электромагнитного излучения и др.
| Векторная диаграмма и МК одномерного АИМ-16 ансамбля сигналов
|
| Сигнально-кодовая конструкция для HDLC-2
|
Рис. 7.10,а. Одномерная ССК, предложенная «PairGain Technologies»
Американская компания «PairGain Technologies» предложила и стандартизовала (ANSI) несколько своих решений по указанной проблеме. Специалистами компании создана система OPTIS (Overlapped PAM Transmission with Interlocking Spectra — совмещенная АИМ-передача с перекрытием спектра), которая представляет собой одномерную СКК для HDSL-2-систем (рис. 7.10).
Рассмотренная выше СКК для HDSL2-системы реализована в аппаратно-программном модуле “HiGain HDSL2”, который обеспечивает удаленный дуплексный доступ по двухпроводной медному кабелю на скорости 1,544 Мбит/сек (прием/передача), и использует в качестве предварительных линейных кодов AMI-, B8ZS- или ZBTSI-коды.
| Выходной
16-уровневый
сигнал СКК
|
Рис. 7.10,б. Одномерная ССК, предложенная «PairGain Technologies»
Высокая стоимость линий связи обуславливает разработку способов и методов, позволяющих одновременно передавать по одной линии связи большое число независимых сообщений, т.е. использовать линию многократно. Такие системы связи называют многоканальными. Связь, осуществляемую с помощью этих систем, принято называть многоканальной. Практически все современные системы связи за редким исключением являются многоканальными.
В современных сетях связи используются аналоговые и цифровые системы передачи(СП) с тенденцией перехода к применению только цифровых систем. Для обеспечения в этих условиях заданных характеристик каналов и трактов, гарантирующих высокое качество передачи информации, принципы проектирования цифровых и аналоговых систем передачи должны быть совместимы.
Основы теории многоканальной передачи сообщений
Используемые методы разделения каналов (РК) можно классифицировать на линейные и нелинейные (комбинационные). В большинстве случаев разделения каналов каждому источнику сообщения выделяется специальный сигнал, называемый канальным. Промодулированные сообщениями канальные сигналы объединяются, в результате чего образуется групповой сигнал. Если операция объединения линейна, то получившийся сигнал называют линейным групповым сигналом.
Для унификации многоканальных систем связи за основной или стандартный канал принимают канал тональной частоты (канал ТЧ или стандартный телефонный канал, СТК), обеспечивающий передачу сообщений с эффективно передаваемой полосой частот 300...3400 Гц, соответствующей основному спектру телефонного сигнала. Многоканальные системы образуются путем объединения каналов ТЧ в группы, обычно кратные 12 каналам. В свою очередь, часто используют «вторичное уплотнение» каналов ТЧ телеграфными каналами и каналами передачи данных. На рис. 8.1 приведена структурная схема наиболее распространенных систем многоканальной связи.
Реализация сообщений каждого источника а1(t), а2(t),...,аN(t) с помощью индивидуальных передатчиков (модуляторов) М1, М2, ..., МN преобразуются в соответствующие канальные сигналы s1(t), s2(t),..., sN(t). Совокупность канальных сигналов на выходе суммирующего устройстваS образует групповой сигнал s(t). Наконец, в групповом передатчикеМсигнал s(t) преобразуется в линейный сигнал sЛ(t), который и поступает в линию связи ЛС.
Допустим, что линия пропускает сигнал практически без искажений и не вносит шумов. Тогда на приемном конце линии связи линейный сигнал sЛ(t) с помощью группового приемника П может быть вновь преобразован в групповой сигнал s(t). Канальными или индивидуальными приемниками П1, П2, ..., ПN из группового сигнала s(t) выделяются соответствующие канальные сигналы s1(t), s2(t), ..., sN(t) и затем преобразуются в предназначенные получателям сообщения а1(t), a2(t), ..., aN(t).
Рис. 8.1. Структурная схема систем многоканальной связи
Канальные передатчики вместе с суммирующим устройством образуют аппаратуру объединения. Групповой передатчикМ, линия связиЛСи групповой приемник Псоставляютгрупповой канал связи (тракт передачи), который вместе с аппаратурой объединения и индивидуальными приемниками составляет систему многоканальной связи. Индивидуальные приемникисистемы многоканальной связи ПK наряду с выполнением обычной операции преобразования сигналов sK(t) в соответствующие сообщения аK(t) должны обеспечить выделение сигналов sK(t) из группового сигнала s(t). Иначе говоря, в составе технических устройств на передающей стороне многоканальной системы должна быть предусмотрена аппаратура объединения, а на приемной стороне — аппаратура разделения.
В общем случае групповой сигнал может формироваться не только простейшим суммированием канальных сигналов, но также и определенной логической обработкой, в результате которой каждый элемент группового сигнала несет информацию о сообщениях источников. Это так называемые системы с комбинационным разделением.
Чтобы разделяющие устройства были в состоянии различать сигналы отдельных каналов, должны существовать определенные признаки, присущие только данному сигналу. Такими признаками в общем случае могут быть параметры переносчика, например амплитуда, частота или фаза в случае непрерывной модуляции гармонического переносчика. При дискретных видах модуляции различающим признаком может служить и форма сигналов. Соответственно различаются и способы разделения сигналов: частотный, временной, фазовый и др.
Частотное разделение сигналов
Функциональная схема простейшей системы многоканальной связи с разделением каналов по частоте представлена на рис. 8.2. В зарубежных источниках для обозначения принципа частотного разделения каналов (ЧРК) используется термин Frequency Division Multiply Access (FDMA, множественный доступ с частотным разделение каналов).
| Генераторы
несущих
частот
|
Рис. 8.2. Функциональная схема системы многоканальной связи с ЧРК
Сначала в соответствии с передаваемыми сообщениями первичные (индивидуальные) сигналы, имеющие энергетические спектры G1(ω), G2(ω), ..., GN(ω) модулируют поднесущие частоты ωK каждого канала. Эту операцию выполняют модуляторы М1, М2, ..., МN канальных передатчиков. Полученные на выходе частотных фильтров Ф1, Ф2, ..., ФN спектры gK(ω) канальных сигналов занимают соответственно полосы частот Dω1, Dω2, ..., DωN, которые в общем случае могут отличаться по ширине от спектров сообщений Ω1, Ω2, ..., ΩN. При широкополосных видах модуляции, например, ЧМ, ширина спектраDωK » 2(b +1)ΩK, т.е. в общем случае Dω³ΩK. Для упрощения будем считать, что используется АМ-ОБП (как это принято в аналоговых СП с ЧРК), т.е. DωК = Ω и Dω = NΩ. Проследим основные этапы образования сигналов, а также изменение этих сигналов в процессе передачи (рис. 8.3).
Будем полагать, что спектры индивидуальных сигналов конечны. Тогда можно подобрать поднесущие частоты ωK так, что полосы Dω1, ..., DωK попарно не перекрываются. При этом условии сигналы sК(t) (k=1,...,N) взаимноортогональны. Затем спектры g1(ω), g2(ω),..., gN(ω) суммируются (S ) и их совокупность g(ω) поступает на групповой модулятор (М). Здесь спектр g(ω) с помощью колебания несущей частоты ω0 переносится в область частот, отведенную для передачи данной группы каналов, т.е. групповой сигнал s(t) преобразуется в линейный сигнал sЛ(t). При этом может использоваться любой вид модуляции.
Рис. 8.3. Преобразование спектров в системе с ЧРК
На приемном конце линейный сигнал поступает на групповой демодулятор(приемникП), который преобразует спектр линейного сигнала в спектр группового сигнала g’(ω). Спектр группового сигнала затем с помощью частотных фильтровФ1, Ф2,...,ФN вновь разделяется на отдельные полосы DωK, соответствующие отдельным каналам. Наконец, канальные демодуляторыДпреобразуют спектры сигналов gK(ω) в спектры сообщений G’K(ω), предназначенные получателям.
Из приведенных пояснений легко понять смысл частотного способа разделения каналов. Поскольку всякая реальная линия связи обладает ограниченной полосой пропускания, то при многоканальной передаче каждому отдельному каналу отводится определенная часть общей полосы пропускания. На приемной стороне одновременно действуют сигналы всех каналов, различающиеся положением их частотных спектров на шкале частот. Чтобы без взаимных помех разделить такие сигналы, приемные устройства должны содержать частотные фильтры. Каждый из фильтров ФK должен пропуститьбез ослабления лишь те частоты ωÎDωK, которые принадлежат сигналу данного канала; частоты сигналов всех других каналов ωÏDωK фильтр должен подавить.
На практике это невыполнимо. Результатом являются взаимные помехимежду каналами. Они возникают как за счет неполного сосредоточения энергии сигнала k-го каналав пределах заданной полосы частотDωK, так и за счет неидеальности реальных полосовых фильтров. В реальных условиях приходится учитывать также взаимные помехи нелинейного происхождения, например за счет нелинейности характеристик группового канала. Для снижения переходных помех до допустимого уровня приходится вводить защитные частотные интервалы Dωзащ (рис. 8.4). Так, например, в современных системах многоканальной телефонной связи каждому телефонному каналу выделяется полоса частот4 кГц, хотя частотный спектр передаваемых звуковых сигналов ограничивается полосой от300до3400Гц, т.е. ширина спектра составляет 3,1 кГц.
Рис. 8.4. Спектр группового сигнала с защитными интервалами
Между полосами частот соседних каналов предусмотрены интервалы шириной по 0,9 кГц, предназначенные для снижения уровня взаимных помех при расфильтровке сигналов. Это означает, что в многоканальных системах связи с частотным разделением сигналов эффективно используется лишь около 80% полосы пропускания линии связи. Кроме того, необходимо обеспечить высокую степень линейности всего тракта группового сигнала.
Временно̀е разделение сигналов
Принцип временного разделения каналов (ВРК) состоит в том, что групповой тракт предоставляется поочередно для передачи сигналов каждого канала многоканальной системы (рис. 8.5). В зарубежных источниках для обозначения принципа временного разделения каналов используется термин Time Division Multiply Access (TDMA, множественный доступ с временным разделением каналов).
Рис. 8.5. Принцип временного разделения каналов
При передаче используется дискретизация во времени (импульсная модуляция). Сначала передается импульс 1-го канала, затем следующего канала и т.д. до последнего канала за номером N, после чего опять передается импульс 1-го канала и процесс повторяется периодически. На приеме устанавливается аналогичный коммутатор, который поочередно подключает групповой тракт к соответствующим приемникам. В определенный короткий промежуток времени к групповой линии связи оказывается подключена только одна пара приёмник/передатчик.
Это означает, что для нормальной работы многоканальной системы с ВРК необходима синхронная и синфазная работа коммутаторов на приемной и передающей сторонах. Для этого один из каналов занимают под передачу специальных импульсов синхронизации. На рис. 8.6 приведены временные диаграммы, поясняющие принцип ВРК. На рис. 8.6,а-в приведены графики трех непрерывных аналоговых сигналов u1(t), u2(t) и u3(t) и соответствующие им АИМ-сигналы. Импульсы разных АИМ-сигналов сдвинуты друг относительно друга по времени. При объединении индивидуальных каналов в канале (линии) связи образуется групповой сигнал с частотой следования импульсов в N раз большей частоты следования индивидуальных импульсов.
Рис. 8.6. Преобразование сигналов при ВРК
Интервал времени между ближайшими импульсами группового сигнала TK называется канальным интерваломили тайм-слотом (time slot). Промежуток времени между соседними импульсами одного индивидуального сигнала называется циклом передачи ТЦ. От соотношения ТЦ и TK зависит число импульсов, которое можно разместить в цикле, т.е. число временных каналов.
При временном разделении так же как и при ЧРК существуют взаимные помехи, в основном обусловленные двумя причинами:
1. первая состоит в том, что линейные искажения, возникающие за счет ограниченности полосы частот и неидеальности амплитудно-частотной и фазо-частотной характеристик всякой физически осуществимой системы связи, нарушают импульсный характер сигналов. При временном разделении сигналов это приведет к тому, что импульсы одного канала будут накладываться на импульсы других каналов. Иначе говоря, между каналами возникают взаимные переходные помехи или межсимвольная интерференция;
2. вторая, взаимные помехи могут возникать за счет несовершенства синхронизации тактовых импульсов на передающей и приемной сторонах.
В силу данных причин временное разделение каналов на основе АИМ не получило практического применения. Временное разделение широко используют в цифровых системах передачи плезиохронной и синхронной иерархий, которые будут подробно рассмотрены ниже.
В общем случае для снижения уровня взаимных помех приходится вводить «защитные» временные интервалы, что соответствует некоторому расширению спектра сигналов. Так, в СП полоса эффективно передаваемых частот F=3100 Гц; в соответствии с теоремой Котельникова минимальное значение частоты дискретизации f0=1/ТД=2F=6200 Гц. Однако в реальных системах частоту дискретизации выбирают с некоторым запасом: f0 = 8 кГц. При временном разделении каналов сигнал каждого канала занимает одинаковую полосу частот, определяемую в идеальных условиях согласно теореме Котельниковаиз соотношения (без учета канала синхронизации)
DtK =T0/N = 1/(2NF ) = 1/(2Fобщ) ,
где Fобщ=FN, что совпадает с общей полосой частот системы при частотном разделении.
Хотя теоретически временное и частотное разделения позволяют получить одинаковую эффективность использования частотного спектра, тем не менее, пока что системы временного разделения уступают системам частотного разделения по этому показателю. Вместе с тем, системы с временным разделением имеют неоспоримое преимущество, связанное с тем, что благодаря разновременности передачи сигналов разных каналов отсутствуют переходные помехи нелинейного происхождения. Кроме того, аппаратура временного разделения значительно проще, чем при частотном разделении, где для каждого индивидуального канала требуются соответствующие полосовые фильтры, которые достаточно трудно реализовать средствами микроэлектроники.
Разделение сигналов по форме
Для разделения сигналов могут использоваться не только такие очевидные признаки, как частота, время и фаза. Наиболее общим признаком сигнала является его форма. Различающиеся по форме сигналы могут передаваться одновременно и иметь перекрывающиеся частотные спектры, но, тем не менее, их можно разделить, если выполняется условие линейной независимости или условие ортогональности.
В настоящее время разработаны новые цифровые методы разделения сигналов по форме, когда в качестве переносчиков различных каналов используются дискретные ортогональные последовательности в виде функций Уолша, Радемахера. В связи с возможностью применения к функциям Уолша логических операций они широко применяются в многоканальных цифровых системах передачи с разделением каналов по форме. Системы многоканальной связи с ортогональными сигналами требуют для нормальной работы той или иной «синхронизации», например, точного совпадения спектра сигнала с полосой пропускания при ЧРК или точного совпадения временных интервалов передачи сигналов при ВРК. В ряде случаев осуществить точную синхронизацию затруднительно. С подобными ситуациями приходится сталкиваться, в частности при организации оперативной связи большого числа подвижных объектов.
Тогда предпочтительными становятся системы асинхронной многоканальной связи, когда сигналы всех абонентов передаются в общей полосе частот, а каналы не синхронизированы между собой. За каждым каналом (абонентом) закрепляется определённая форма сигнала, которая и является отличительным признаком («адресом») данного абонента. При обычном разделении по форме условие ортогональности выполняется лишь тогда, когда для всех каналов существует единая тактовая синхронизация. В асинхронной многоканальной системе для обеспечения полного линейного разделения сигналов ортогональность (или, по крайней мере, линейная независимость) между любой парой сигналов должна сохраняться при любом сдвиге во времени.
Это значит, что для пары сигналов Si(t) и Sj(t) должно выполняться условие:
(Si(t), Sj(t)) = 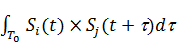 = 0 , i ¹ j ,
= 0 , i ¹ j ,
при 0 £ t £ Т0, где Т0 — длительность сигнала. Интегрирование производится на любом интервале времени длительностью Т0. Можно сказать, что рассмотренное равенство выполняется только в том случае, когда Si(t) представляет собой белый шум, то есть имеет неограниченную ширину спектра и бесконечную дисперсию. Для реальных сигналов это невыполнимо. Можно, однако, построить сигналы, для которых указанное равенство выполняется приблизительно. То есть скалярное произведение (Si(t), Sj(t+t)) при любом сдвиге много меньше энергии элемента сигнала:
(Si(t), Sj(t + t)) << 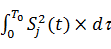 .
.
Эти сигналы можно назвать «почти ортогональными» (квазиортогональными). На основании ранее сказанного можно предположить, что такие сигналы должны иметь очень широкий спектр, или точнее большую базу(произведение DFT0).
Основной особенностью подобных сигналов, получивших название шумоподобных сигналов (ШПС), является равномерность энергетического спектра и d-образная форма (острый пик) автокорреляционной функции (АКФ). Свойствами ШПС обладают псевдослучайные последовательности (ПСП), последовательности Баркера и др. При передаче ПСП по высокочастотному каналу обычно применяется фазовая манипуляция несущей со сдвигом фазы на1800.
Другой разновидностью ШПС являются сигналы, формируемые с помощью частотно-временной матрицы (ЧВМ, рис. 8.7). «Адрес» каждого канала (абонента) можно сформировать из набора «элементарных площадок» частотно-временного пространства. При этом в каждом наборе могут использоваться только те элементарные сигналы («площадки»), которые относятся к разным строкам и столбцам. Число различных перестановок элементов квадратной ЧВМ размером М´М с учётом указанного выше ограничения определяет количество отличающихся друг от друга последовательностей длиной М. Это число равно М!. Однако не все из полученных сигналов обладают достаточно хорошими авто- и взаимокорреляционными свойствами.
Наличие у сигналов совпадающих позиций ухудшает их взаимокорреляционные свойства, поэтому используются не все комбинации ЧВМ. Максимальное количество комбинаций, для которых уровень боковых лепестков корреляционных функций не превышает
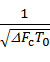 ,
,
приближается к DFсT0.
Комбинационное разделение сигналов
| Рис. 8.7. Пример ЧВМ (7´7)
|
Сущность комбинационного способа формирования группового сигнала состоит в следующем. Пусть сообщения, поступающие на устройство уплотнения от N источников, представлены символами m-ичного кода (m³2). Предположим, что символы всех источников имеют одинаковую длительность и одновременно, по одному символу от каждого источника, поступают на устройство уплотнения. Тогда число состояний комбинаций символов от всех источников равно mN. Таким образом, применяя основание кода mN, можно одновременно передавать информацию от N индивидуальных каналов. Групповой сигнал представляет собой отображение определённой комбинации сигналов различных каналов. Разделение сигналов, основанное на различии комбинаций сигналов разных каналов, называется комбинационным.
Таблица 8.1
Дата добавления: 2016-01-03; просмотров: 1114;
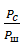 ) .
) .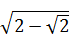 = 0.765 , d1 =
= 0.765 , d1 = 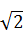 = 1.414 ,
= 1.414 ,
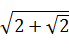 = 1.848 , d3 = 2 .
= 1.848 , d3 = 2 .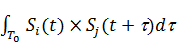 = 0 , i ¹ j ,
= 0 , i ¹ j ,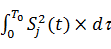 .
.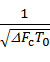 ,
,