Методические рекомендации и последовательность выполнения. Задание выполняется на формате А3 в масштабе 1:2.

Задание выполняется на формате А3 в масштабе 1:2.

Пример выполненного задания см. на рисунке 1.

В примере рассматривается развертка призмы способами нормального сечения и раскатки.

1. Вначале необходимо перечертить горизонтальную и фронтальную проекции фигуры (в уменьшенном масштабе). Далее необходимо определить натуральную величину всех прямых и плоскостей, входящих в состав многогранника. Для этого необходимо проанализировать их положение относительно плоскостей проекций. Натуральную величину сечения наклонной плоскостью следует найти способом замены плоскостей проекций и способом вращения вокруг проецирующей прямой. Если в варианте присутствуют несколько наклонных сечений, то для каждого из них выбрать один из способов, но различные.

2. Задняя грань призмы параллельна фронтальной плоскости проекции, поэтому переносим ее в соответствии с размерами в горизонтальной связи правее. К ней достраиваем оставшиеся три грани боковой поверхности. Заметим, что два основания призмы и сечение 6-7-8-11-12 параллельны горизонтальной плоскости проекции, следовательно, натуральные величины необходимых отрезков замеряем с горизонтальных проекций. К развертке боковой поверхности перпендикулярно пристраиваем натуральную величину сечения в наклонной плоскости и часть верхнего основания.

3. В горизонтальной связи с горизонтальной проекцией переносим многоугольник 6-7-8-11-12. К нему пристраиваем в соответствующие направления боковые прямоугольники сквозного паза. Заметим, что отрезки 6-5, 12-13, а также 8-9, 11-10 равны между собой и параллельны фронтальной плоскости проекции, поэтому их натуральную величину замеряем с фронтальной проекции. С целью более рационального раскроя листового материала части нижнего основания (прямоугольные треугольники) соединяем с полученной разверткой поверхности сквозного паза.

Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов в призме, тем точнее развертка (при n → ∞призма преобразуется в цилиндр). При выполнении развертки цилиндра рекомендуется вписывать 12-угольную призму.

4. Обвести основной контур, оставив линии построения тонкими. Линии сгиба – штрих - пунктирная с двумя точками тонкая. Заполнить штамп основной надписи.

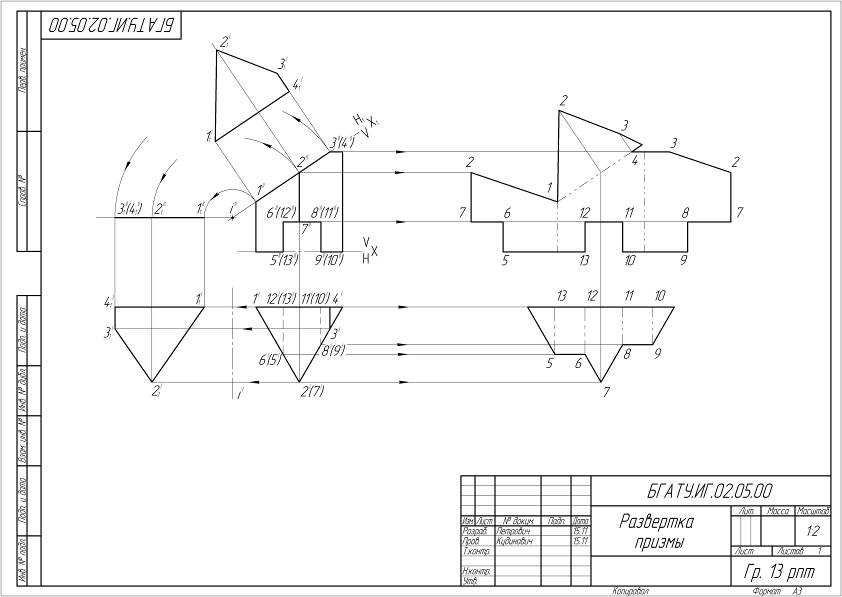
Рисунок 1 – Пример выполнения задания «Развертка призмы».