ГЕОМЕТРИЧЕСКИЕ ТЕЛА
Цель: усвоить способы образования поверхностей (многогранных и вращения), развить навыки изображения геометрических тел на проекционном комплексном чертеже и аксонометрии.
Задание: по заданному условию выполнить проекционный комплексный чертеж и аксонометрию призмы или цилиндра со срезами, построить натуральную величину наклонного сечения.
 Теоретические сведения
Теоретические сведения
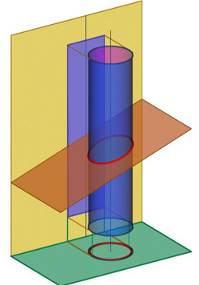
Пересечение цилиндра плоскостью (рис. 1.1).
При пересечении цилиндра вращения плоскостью возможны случаи:
- секущая плоскость параллельна оси - в сечении цилиндрической поверхности получаются две прямые (образующие) (рисунок 1.2а);
- секущая плоскость перпендикулярна оси - в сечении получается окружность, равная окружностям оснований (рисунок 1.2б);
- секущая плоскость наклонна к оси - в сечении получается эллипс, малая ось которого всегда равна диаметру цилиндра, а большая зависит от угла j (рисунок 1.2в).
Рисунок 1.1 -Пересечение цилиндра плоскостью
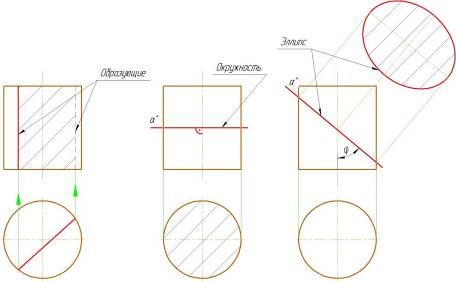
а б в
Рисунок 1.2 -Пересечение цилиндра плоскостью
На рисунке 2 показано построение проекций линии пересечения прямого цилиндра плоскостью Q (Q"), T (T") и Р (Р") .
Горизонтальная плоскость Р (Р") пересекает поверхность цилиндра по части окружности, профильная плоскость T (T") по прямым АВ и CD (образующим цилиндра), фронтально-проецирующая плоскость Q (Q") - по части эллипса. Фронтальная проекция линий пересечения совпадает со следами - проекциями секущих плоскостей (P ", T ", Q"), а горизонтальная — с окружностью оснований цилиндра.
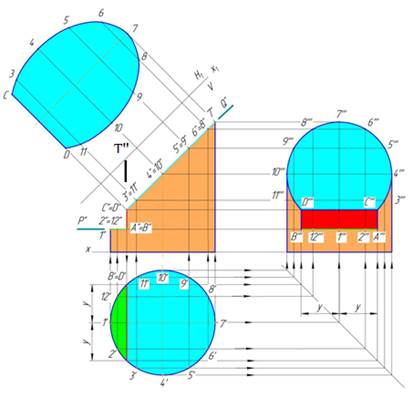
Рисунок 2 - Построение проекций усеченной части цилиндра
Построение профильной проекции сводится к построению профильных проекций точек по двум заданным, направление построений линий связи указано стрелками. Вместо ломаных линий связи при построении профильных проекций точек можно использовать координаты y, которые откладываются на горизонтальных линиях связи по разные стороны оси цилиндра (см. построение точек А, В, С, D).
Обычно для построения точек линий сечения пользуются образующими, равноотстоящими друг от друга. Поэтому горизонтальная проекция цилиндра (окружность) разделена на 12 частей (точки 1, 2... 12). Этой равномерной «разметкой» удобно пользоваться не только для построения проекций сечений, но и для построения развертки.
Действительный вид фигуры сечения плоскостью Q построен способом перемены плоскостей проекций. Новая ось проекций Х1 проведена параллельно следу - проекции Q".Выполнив соответствующие построения на плоскости H1, получим натуральную величину сечения цилиндра плоскостью Q.
Пересечение призмы проецирующими плоскостями.
При пересечении многогранника (рис. 3) плоскостью в сечении получается многоугольник, вершинами которого являются точки пересечения ребер многогранника плоскостью, а сторонами – отрезки прямых, по которым грани многогранника пересекаются этой плоскостью.
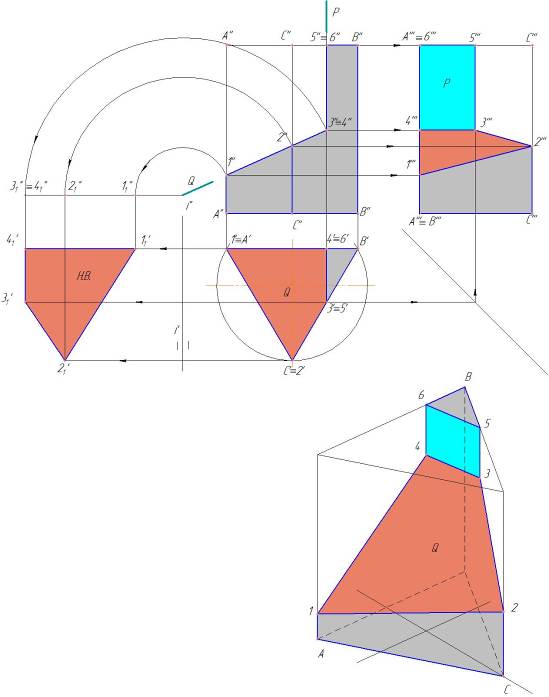
Рисунок 3 – Построение проекций линии пересечения прямой
треугольной призмы фронтально – проецирующими плоскостями
Определение вершин многоугольника сводится к построению точек пересечения прямых (ребер многогранника) с плоскостью – способ ребер.
При определении сторон многоугольника решаются задачи на пересечение двух плоскостей – способ граней.
Правильная треугольная призма усечена двумя плоскостями: фронтально-проецирующей Q(Q¢¢) и профильной P(P¢¢) (рисунок ). Построить профильную проекцию усеченной призмы.
Плоскость Q пересекает верхнее основание призмы по прямой 4-5, а боковую поверхность по горизонтально-проецирующим прямым 1-5 и 3-4. Прямая 1-5 совпадает с ребром А призмы.
Плоскость Q пересекает ребро А призмы в точке 1, а ребро С–в точке 2.
Плоскости Q и P пересекаются по линии 1-3.
Профильные проекции указанных выше точек определяются при помощи линий связи. Соединив построенные точки получим профильную проекцию линии пересечения.
Плоскости Q и P пересекаются по фронтально-проецирующей прямой 3-4. Соединив построенные проекции точек получим проекции линии пересечения.
Натуральная величина многоугольника сечения найдена способом вращения вокруг фронтально-проецирующей оси.
Проекция 11',21',31',41' – натуральная величина многоугольника сечения (это четырехугольник 1, 2, 3, 4).
Дата добавления: 2016-01-26; просмотров: 1204;
