СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА

Цель способов преобразования чертежа – приведение геометрических фигур в частное (параллельное или проецирующее) положение относительно плоскостей проекций для обеспечения большей наглядности изображения и упрощения решения позиционных и метрических задач.

Способы преобразования можно классифицировать, исходя из основных составляющих аппарата проецирования:

- изменение положения фигур относительно основной системы координат (способ вращения относительно различных осей; способ плоскопараллельного перемещения);

- изменение положения плоскостей проекций (способ замены плоскостей проекций).

1. Способ вращения.

Сущность способа вращения заключается в том, что прямую линию плоскую фигуру или пространственную форму поворачивать вокруг выбранной оси до частного положения, при этом система плоскостей проекций не изменяется.

В зависимости от выбранного положения оси вращения по отношению к плоскостям проекций различают:

1.1 Вращение вокруг проецирующих прямых;

1.2 Вращение без указания положения оси вращения (плоскопараллельное перемещение);

1.3 Вращение вокруг линии уровня (горизонтали, фронтали).

1.1 При вращении точки вокруг оси, перпендикулярной одной из плоскостей проекций, точка в пространстве описывает окружность, при этом одна ее проекция перемещается по окружности, а вторая – по прямой, параллельной осям координат (рис. 1).

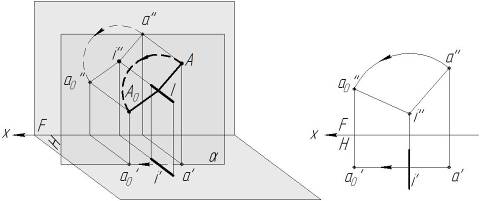
Рисунок 1 – Вращение точки вокруг проецирующей прямой

При вращении отрезка прямой вокруг оси, перпендикулярной одной из плоскостей проекций, проекция отрезка на этой плоскости проекций не изменяет своей величины, а изменяется лишь ее положение относительно оси проекций. Вторая проекция отрезка при его вращении изменяет величину и положение (исключение – вращение на 180°) (рис. 2).

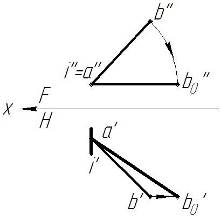
Рисунок 2 – Вращение отрезка вокруг проецирующей прямой

Если плоскость задана на проекционном комплексном чертеже одним из известных способов, то вращение плоскости вокруг оси осуществляется поворотом на один и тот же угол в одном и том же направлении точек и прямых, которыми задана плоскость.

На рис. 3 показано преобразование плоскости (треугольника ABC) способом вращения вокруг проецирующей прямой. Для начала в плоскости необходимо построить линию уровня (горизонталь с''1'' и с'1'). Далее через точку прохождения линии уровня (точка с'') провести ось вращения (i₁'', i₁'), перпендикулярную горизонтальной плоскости проекций. Вращать треугольник АВС следует до момента, когда горизонталь с'1' станет перпендикулярна оси проекций (ось х). На фронтальной проекции проводим горизонтальные линии движения от всех точек треугольника АВС до пересечения с вертикальными линиями связи с горизонтальной проекции. После первого преобразования треугольник АВС занимает фронтально-проецирующее положение (линии а₁''с₁''b₁'' и треугольник а₁'с₁'b₁'). Теперь вводим вторую ось вращения (i₂'', i₂'), перпендикулярную горизонтальной плоскости проекций. Вращаем все точки треугольника АВС до положения, параллельного горизонтальной плоскости (b₂''с₂''а₂''). На горизонтальной проекции проводим линии направления движения до пересечения с линиями связи с фронтальной проекции. Треугольник а₂'с₂'b₂' – натуральная величина треугольника АВС.

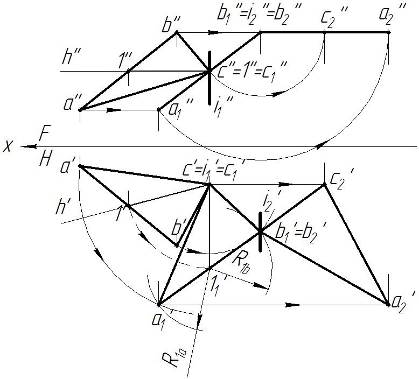
Рисунок 3 – Вращение плоскости вокруг проецирующей прямой

1.2 Так как при вращении объектов вокруг оси, перпендикулярной одной из плоскостей проекций, их проекции на данную плоскость не изменяют своей формы и величины, то можно производить вращение, не указывая положения оси вращения (рис. 4, 5).

На рис. 4 изображен отрезок АВ в общем положении, ни одна из его проекций не отображает натуральной величины. Способ вращения подразумевает изменение положения объекта из общего в частное, поэтому рядом с исходным изображением проводим на фронтальной проекции линию, параллельную горизонтальной проекции (или оси х), и отмечаем на ней длину проекции a''b'', получаем новую проекцию a₁''b₁'', от которой проводим линии связи. От горизонтальной проекции a'b' проводятся линии параллельного переноса до пересечения с вертикальными линиями связи, в местах пересечения получаем точки для новой проекции a₁'b₁'. Проекция a₁'b₁' – есть натуральная величина отрезка АВ.

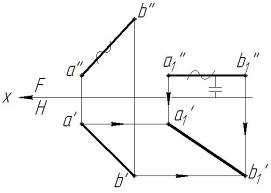
Рисунок 4 – Вращение отрезка без указания оси вращения

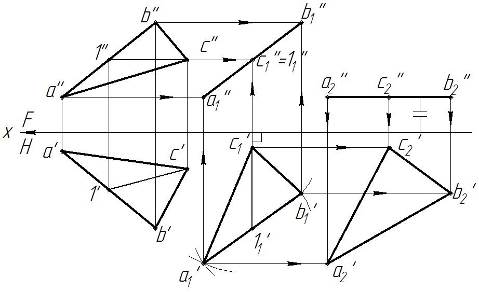
Рисунок 5 – Вращение плоскости без указания оси вращения

При преобразовании чертежа плоскости способом плоскопараллельного перемещения все действия с проекциями плоскости повторяются аналогично преобразованию способом вращения вокруг проецирующей линии. На рис. 5 дана плоскость АВС в общем положении. На фронтальной проекции проводится линия уровня (горизонталь с''1'') и проецируется на горизонтальную проекцию с'1'. Далее на горизонтальной проекции рядом с основным изображение вычерчивается новая горизонтальная проекция а₁'b₁'с₁' плоскости АВС перпендикулярно фронтальной плоскости проекций (горизонталь с'1' должна быть перпендикулярна оси х). От нее проводятся линии связи, а от фронтальной проекции плоскости АВС линии параллельного переноса до пересечения с линиями связи. На фронтальной плоскости проекций плоскость АВС преобразовывается в прямую линию а₁''с₁''b₁''. На фронтальной проекции строим новую проекцию а₂''с₂''b₂'' плоскости АВС параллельно горизонтальной плоскости проекций (параллельно оси х), от нее проводим линии связи на горизонтальную плоскость проекций. На горизонтальной плоскости проводим линии параллельного переноса от предыдущей проекции а₁'b₁'с₁' плоскости АВС до пересечения с линиями связи. Горизонтальная проекция а₂'с₂'b₂' – есть натуральная величина плоскости АВС.

1.3 Вращение вокруг линии уровня применяется в случаях, когда необходимо получить положение фигуры, параллельное той или иной плоскости проекций (натуральную величину).

На рис. 6 показан способ вращения вокруг линии уровня для нахождения натуральной величины треугольника АВС. Для этого проводим фронталь c'1', c''1''. Опускаем перпендикуляр из точки a'' к фронтали. Отмечаем точку o'' (прямая a''o'' является радиусом вращения точки А вокруг фронтали С1). Определяем натуральную величину радиуса a''o'' методом прямоугольного треугольника. Поворачиваем точку a₀ относительно точки o'' до пересечения с продолжением перпендикуляра a''o''. Отмечаем точку А. Из точки А проводим прямую через точку 1''. Из точки b'' проводим перпендикуляр к фронтали c''1''. В месте пересечения отмечаем точку В. Соединяем точки А, В, С – натуральная величина треугольника АВС найдена.

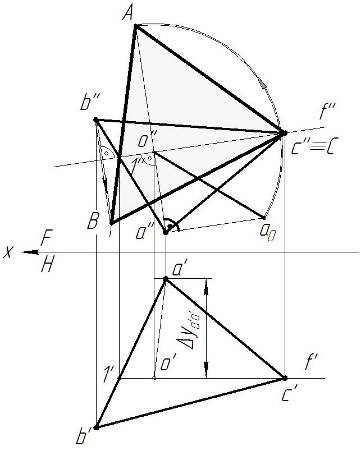
Рисунок 6 – Вращение вокруг линии уровня

2. Способ замены плоскостей проекций.

Суть способа замены плоскостей проекций заключается в выборе такой системы плоскостей проекций, при которой объект преобразования оказался бы в частном положении (рис. 7).

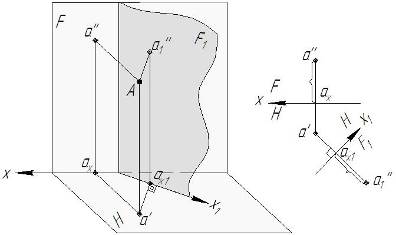
Рисунок 7 – Способ замены плоскостей проекций

На рис. 8 показано преобразование отрезка АВ способом замены плоскостей. Даны две проекции a'b' и a''b'' отрезка общего положения АВ. Нужно ввести новую систему координат таким образом, чтобы отрезок АВ находился в частном положении (для нахождения натуральной величины отрезок должен быть параллельным одной из плоскостей проекций). Для этого введем новую фронтальную плоскость F₁ так, чтобы отрезок АВ стал ей параллелен (новая ось х₁ должна быть параллельна горизонтальной проекции a'b'). Далее проводим линии связи на новую фронтальную плоскость проекций F₁ (линии связи перпендикулярны оси х₁). По этим линиям связи откладываем расстояние от оси х до точек a'' и b''. Полученная проекция a₁''b₁'' – есть натуральная величина отрезка АВ.

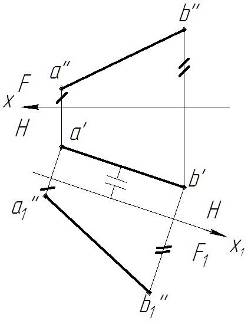
Рисунок 8 – Нахождение натуральной величины отрезка способом замены плоскостей проекций

На рис. 9 показано преобразование плоскости общего положения АВС способом замены плоскостей проекций. На фронтальной проекции проводится линия уровня (горизонталь с''1'') и проецируется на горизонтальную проекцию с'1'. Далее на горизонтальной проекции вводится новая фронтальная плоскость F₁ таким образом, чтобы новая ось х₁ была перпендикулярна горизонтали с'1'. Далее проводим линии связи на новую фронтальную плоскость проекций F₁ (линии связи перпендикулярны оси х₁). По этим линиям связи откладываем расстояние от оси х до точек a'', b'' и с''. На фронтальной плоскость АВС преобразовывается в прямую линию а₁''с₁''b₁''. На фронтальной плоскости проекций F₁ вводим новую горизонтальную плоскость проекций Н₁ таким образом, чтобы фронтальная проекция а₁''с₁''b₁'' была ей параллельна (а₁''с₁''b₁'' должна быть параллельна новой оси х₂). Далее проводим линии связи на новую горизонтальную плоскость проекций Н₁ (линии связи перпендикулярны оси х₂). По этим линиям связи откладываем расстояние от оси х₁ до точек a', b' и с'. Горизонтальная проекция а₁'b₁'с₁' – есть натуральная величина плоскости АВС.

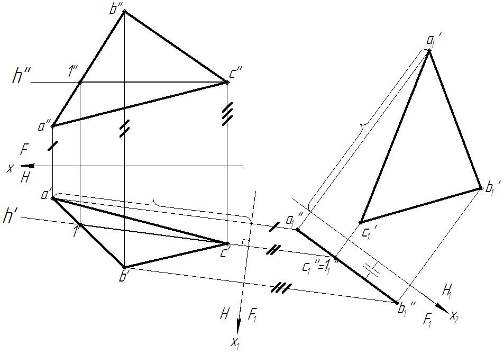
Рисунок 9 – Нахождение натуральной величины треугольника способом замены плоскостей проекций