Основные определения 5 страница
Рис. 6.19. Решётчатая диаграмма ССК (1/2)
Рассмотрим в общем виде процедуру декодирования свёрточных кодов. Схема передачи, состоящая из кодирующего и декодирующего устройств, представлена на рис. 6.20.
| Eи |
| F(x) |
| F(x) |
| Информационные символы |
| Информационные символы |
| Проверочные символы |
| Исправляющая последовательность |
| Eп |
Рис. 6.20. Схема передачи с использованием ССК (1/2)
К общим методам декодирования (то есть обнаружения и исправления возможных ошибок) свёрточных кодов относится декодирование по максимуму правдоподобия (алгоритм Витерби) и последовательное декодирование.
Идея алгоритма Витерби состоит в том, что необходимо по принятой кодовой последовательности восстановить на приёмной стороне путь кодера по решётчатой диаграмме.
Из рис. 6.18 и 6.19 видно, что кодер не может переходить из одного состояния во все возможные состояния. Поэтому некоторые переходы считаются запрещёнными. Фактически на приёмной стороне регенерируется работа кодера по входной информационной последовательности (рис. 6.20). Таким образом, если в принятой последовательности будет ошибка, то она приведёт к появлению запрещённого перехода. Если же закодированная последовательность не будет искажена помехами в канале, то приёмный кодер полностью повторит работу передающего кодера.
Сущность правила максимального правдоподобия заключается в том, что некорректный путь в диаграмме будет содержать запрещённый переход. Этот путь будет расположен между несколькими возможными корректными путями. Среди этих корректных путей считается правильным тот, к которому «ближе всего» (в смысле выбранной метрики) расположен некорректный путь.
Системы с обратной связью
Нередко встречаются случаи, когда информация может передаваться не только от одного абонента к другому, но и в обратном направлении. В таких условиях появляется возможность использовать обратный поток информации для существенного повышения верности сообщений, переданных в прямом направлении. При этом не исключено, что по обоим каналам (прямому и обратному) в основном непосредственно передаются сообщения в двух направлениях («дуплексная связь») и только часть пропускной способности каждого из каналов используют для передачи дополнительных данных, предназначенных для повышения верности.
Возможны различные способы использования системы с обратной связью в дискретном канале. Обычно их подразделяют на два типа: системы с информационной обратной связью и системы с управляющей обратной связью.
Системами с информационной обратной связью (ИОС) называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения:
1. повторить ошибочно принятые отрезки сообщения;
2. изменить применяемый код (передав предварительно соответствующий условный сигнал и убедившись в том, что он принят);
3. прекратить передачу при плохом состоянии канала до его улучшения.
В системах с управляющей обратной связью (УОС) приемное устройство на основании анализа принятого сигнала само принимает решение о необходимости повторения, изменения способа передачи, временного перерыва связи и передает об этом указание передающему устройству.
Возможны и смешанные методы использования обратной связи, когда в некоторых случаях решение принимается на приемном устройстве, а в других случаях на передающем устройстве на основании полученной по обратному каналу информации. Наиболее распространены системы с обнаружением ошибок. Такие системы часто называют системами с автоматическим перезапросом ошибок (ARQ, Automatic ReQuest).
| Глава 7 | Сигнально-кодовые конструкции |
Одним из направлений повышения частотно-энергетической эффективности систем передачи информации является разработка и применение сигнально-кодовых конструкций (СКК). Идея построения таких конструкций состоит в увеличении минимального евклидова расстояния между разрешёнными сигнальными последовательностями с использованием избыточности кодирования.
Из всего многообразия СКК наибольшее внимание привлекают конструкции на основе решётчатых кодов (СКК РК), важный класс которых составляют свёрточные коды. Мягкое декодирование СКК РК по алгоритму Витерби обеспечивает асимптотический выигрыш от кодирования 3…7 дБ. О практической значимости СКК РК свидетельствует их применение в Рекомендациях ITU-T V.32, V.33, V.34.
Скорость передачи
Сигналы в форме последовательностей элементов одинаковой длительности называются изохронными (iso — равный). Все остальные сигналы, которые не удовлетворяют этому условию, называются неизохронными (анизохронными). Имеются, однако, неизохронные сигналы, которые приближенно в течение некоторого времени изохронны (например, стартстопные сигналы на интервалах между стартом и стопом). Два сигнала называются синхронными (syn — вместе), если их значащие моменты имеют желаемые фазовые соотношения.
Количество единичных элементов сигнала в секунду есть скорость передачи элементов сигнала (скорость модуляции)
V = 1/ Т0 ,
где Т0 — длительность единичного элемента сигнала — единичный интервал в секундах. Единица скорости V имеет размерность 1/с и называется «Бод» (международное обозначение Bd) по имени французского инженера Бодо.
Широкое практическое применение находит ещё одна характеристика — скорость передачи символов, под которой понимается количество символов в единицу времени. Эта скорость обычно измеряется числом двоичных символов (бит) в секунду (бит — bit, сокращенно от английского binary digit — двоичный символ).
Установим соответствие между двумя выше названными характеристиками скорости, полагая, что символ кода отображается элементом сигнала длительностью Т0. Если символы кода двоичные (основание кода m=2), то элемент сигнала «несёт» информацию об одном двоичном символе (один бит). Тогда скорость передачи в бодах численно равна скорости в бит/с. Если символы кода принимают m значений(m-ичный код), то и элемент сигнала должен иметь m дискретных состояний. Теперь каждый элемент сигнала будет «нести» информацию оlog2m битах(при m=2log2m = 1 бит). Таким образом, если скорость передачи элемента сигнала, принимающего m состояний, V Бод, то скорость передачи символов
B[бит/с] = V log2m .
Как известно, для передачи импульсов прямоугольной формы необходима бесконечная полоса пропускания. Ограничение полосы частот в реальных каналах связи вызывает нежелательное искажение формы импульсов, их взаимное наложение — межсимвольную интерференцию. Искажение формы прямоугольных импульсов зависит от того, насколько узка полоса пропускания, или, с другой стороны, от того, с какой скоростью осуществляется передача по каналу связи с заданной полосой пропускания. Влияние межсимвольной интерференции, имеющей место при длительности элемента сигнала, большей Т0, можно существенно ослабить (в принципе даже свести к нулю), если решения о переданных кодовых символах принимать на основании анализа значений процесса на выходе канала лишь в отчётных точках
ti = iT0 .
Для того чтобы воздействие соседних импульсов не проявлялось в моменты ti = iT0, необходимо и достаточно, как показал Гарри Найквист (американский учёный в области теории информации), чтобы форма импульса g(t) удовлетворяла условию
g(nT0 – mT0) = 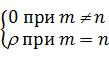 .
.
Такой сигнал в момент отсчёта имеет отличное от нуля значение r и нули во всех остальных отсчётных точках. Согласно теореме Котельникова (российский учёный в области теории информации) это импульс видаsinx/x:
g(t) = r × 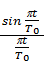 .
.
Спектр импульса A(F)определяется выражением:
A(F) = 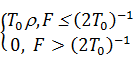 .
.
Функции g(t) и A(F) представлены на рис. 7.1 (для b = 0).
| A(F) |
| F |
| 1/T0 |
| 1/2T0 |
| 0 |
| ρT0 |
| ρT0 /2 |
| β = 0 |
| β = 1 |
| β = 0,5 |
| β = 0,25 |
Рис. 7.1,а. Функции A(F) и g(t)
Таким образом, для импульсов формы sinx/x в полосе частот DF = 1/2T0 можно обеспечить скорость передачи V = 1/T0. Скорость
Vmax = 2DF
является максимальной. Это выражение представляет собой фундаментальный вывод из теории связи:максимальная скорость передачи (1/Т0)max, достигаемая при передаче в полосе низких частот при отсутствии межсимвольной интерференции, численно в два раза больше ширины полосы. Эту скорость передачи Vmax иногда называют «скоростью передачи по Найквисту» («предел Найквиста»).
| T0 |
| β = 0,5 |
| g(t) |
| 2T0 |
| t |
| -2T0 |
| -T0 |
| 0 |
| β = 0,25 |
| β = 0 |
| ρ |
Рис. 7.1,б. Функции A(F) и g(t)
Для двоичных сигналов это означает, что удельная скорость передачи символов
В0[бит×с-1/Гц] = 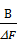 ,
,
то есть скорость B в расчёте на 1 Гц не может превзойти значение 2 бит×с-1/Гц.
Импульс видаsin(pt/T0)/(pt/T0)занимаетминимальную полосу частот1/2Т0, что и даёт значение Vmax. Такую форму импульса можно получить на выходе канала, имеющего частотную характеристику идеального фильтра нижних частот с прямоугольной амплитудно-частотной характеристикой (АЧХ) (рис. 7.1,а, b=0).
Реально АЧХ имеет не прямоугольную форму, а скруглённую. В цифровых системах передачи это скругление осуществляется по закону «приподнятого косинуса». В результате спектр вместо прямоугольной формы приобретает форму (рис. 7.1,а):
A(F) = 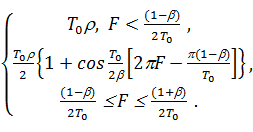
Коэффициент сглаживания b задаётся в пределах 0 £ b £ 1. Так что максимально спектр может быть на 100% шире полосы Найквиста1/2T0. Форма импульса (рис. 7.1,б), имеющая вид:
g(t) = r× 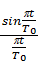 ´
´ 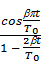 ,
,
удовлетворяет условию Найквиста. Как известно, вероятность ошибочного приёма в конкретной системе определяется отношением Еб/N0. Предыдущее неравенство показывает, что возрастание удельной скорости передачи требует увеличение энергетических затрат(Еб) на один бит, что иллюстрирует рис. 7.3. Так как теперь занимаемая полоса DF = (1+b)/2T0, то максимально достижимая по Найквисту удельная скорость передачи для двоичных сигналов будет2/(1+b) бит×с-1/Гц. Величина 2 бит×с-1/Гц является предельной для двоичных сигналов (m = 2), когда элементарный сигнал соответствует двоичному символу. В общем случае передачи m-ичных символов, когда каждый элемент сигнала «переносит» log2m бит, удельная скорость передачи двоичных символов В0 бит×с-1/Гц может быть увеличена. Такая принципиальная возможность роста В0 за счёт повышения m требует выполнения условияlog2m >½В0 .
Рассмотрим пример, когда по каналу с полосойDF =3 кГц требуется передать последовательность двоичных символов, поступающих на его вход со скоростью 9600 бит/с. Это значит, что необходимо обеспечить удельную скорость передачи В0 = 9600/3000 = 3,2 бит×с-1/Гц. Применяя для передачи двоичные сигналы, можно достичь удельной скорости передачи В0 = 2 бит×с-1/Гц . Для передачи необходимо использовать m-ичные сигналы. Из неравенства log2m >½В0 находим m = 4. Для этого укрупняем двоичную последовательность символов, объединяя их по два символа в блок. Блок из двух символов (0, 1) может принимать четыре вида: 11, 10, 00, 01, которые обозначим 0, 1, 2, 3. Таким образом, на основе блокового укрупнения осуществляется однозначное преобразованиедвоичной последовательности (m = 2) в последовательность 4-ичных чисел (m = 4), имеющих пониженную в два раза скорость(рис. 7.2). Каждому символу 0, 1, 2, 3 для передачи соответствует свой сигнал:
0 ® s1(t), 1 ® s2(t) ,
2 ® s3(t), 3 ® s4(t) .
В общем случае скорость V снижается в log2m раз. Именно в этом состоит физический смысл принципиальной возможности увеличения В0.
| t |
| t |
Рис. 7.2. Однозначное преобразование двоичной последовательности
Дата добавления: 2016-01-03; просмотров: 777;
