Основные определения 4 страница
Если длина кода n задана, то можно получить любое значение d, не превышающее n, уменьшая число комбинаций М. Поэтому задачу поиска наилучшего кода (в смысле максимального d) следует формулировать так: при заданных M и n найти код длины n, содержащий М комбинаций и имеющий наибольшее возможное d. В общем виде эта задача в теории кодирования не решена, хотя для многих значений n и М ее решения получены.
На первый взгляд помехоустойчивое кодирование реализуется весьма просто. В память кодирующего устройства (кодера) записываются разрешенные кодовые комбинации выбранного кода и правило, по которому с каждым из М сообщений источника сопоставляется одна из таких комбинаций. Данное правило известно и декодеру.
Получив от источника определенное сообщение, кодер отыскивает соответствующую ему комбинацию и посылает ее в канал. В свою очередь, декодер, приняв комбинацию, искаженную помехами, сравнивает ее со всеми М комбинациями списка и отыскивает ту из них, которая ближе остальных к принятой.
Однако даже при умеренных значениях n такой способ весьма сложный. Покажем это на примере. Пусть выбрана длина кодовой комбинации n=100, а скорость кода примем равной 0,5(число информационных и проверочных символов равно). Тогда число разрешенных комбинаций кода будет 250>>1015. Соответственно размер таблицы будет 100×1015=1017 бит >> 1016 байт = 10000 Тбайт.
Таким образом, применение достаточно эффективных (а значит, и достаточно длинных) кодов при табличном методе кодирования и декодирования технически невозможно.
Поэтому основное направление теории помехоустойчивого кодирования заключается в поисках таких классов кодов, для которых кодирование и декодирование осуществляются не перебором таблицы, а с помощью некоторых регулярных правил, определенных алгебраической структурой кодовых комбинаций.
Линейные коды
Одним из таких классов являются линейные блоковые коды. Линейными называются такие двоичные коды, в которых множество всех разрешенных блоков является линейным пространством относительно операции поразрядного сложения по mod2.
Если записать k линейно-независимых блоков в виде k строк, то получится матрица размером n´k, которую называют порождающей или производящей матрицей кода G.
Множество линейных комбинаций образует линейное пространство, содержащее 2k блоков, т.е. линейный код, содержащий 2k блоков длиной n, обозначают (n, k). При заданных n и k существует много различных (n, k)-кодов с различными кодовыми расстояниями d, определяемых различными порождающими матрицами. Все они имеют избыточность ek=1 - k/n или относительную скорость Rk=k/n.
Чаще всего применяют систематические линейные коды, которые строят следующим образом. Сначала строится простой код длиной k, т.е. множество всех k-последовательностей двоичных символов, называемых информационными. Затем к каждой из этих последовательностей приписывается r = n – k проверочных символов, которые получаются в результате некоторых линейных операций над информационными символами.
Простейший систематический код (n,n-1) строится добавлением к комбинации из n-1информационных символов одного проверочного, равного сумме всех информационных символов по модулю 2. Такой код (n,n-1) имеет d=2 и позволяет обнаружить одиночные ошибкии называется кодом с одной проверкой на четность.
Положим, что исходные комбинации ak первичного кода: 001, 010, 011, 100, 101, 110, 111(k=3). И выберем следующую порождающую матрицу для (5,3)-кода:
G = 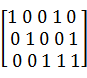 .
.
Тогда каждую комбинацию (5,3)-кода можно вычислить по следующей формуле:
an = ak ´ G .
Например, кодовой комбинации 001будет соответствовать кодовая комбинация an линейного кода:
a5 = 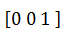 ´
´ 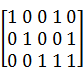 =
= 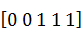 .
.
Аналогичным образом можно найти и остальные комбинации (5,3)-кода. Таким образом, порождающая матрица G является сжатым описанием линейного кода.
Матрица Н, удовлетворяющая условию: G´HT = 0, называется проверочной матрицей кода. Она имеет размерность (n - k)´n. Для матрицы G, рассмотренной в предыдущем примере, матрица Н имеет вид:
H = 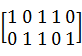 .
.
Матрица Н позволяет не только проверить, принадлежит ли комбинация an коду, но и формировать эти комбинации при кодировании. Преимуществом линейных, в частности систематических, кодов является то, что в кодере и декодере не нужно хранить большие таблицы всех кодовых комбинаций, а при декодировании не нужно производить большое количество сравнений.
Однако для получения высокой верности связи следует применять коды достаточно большой длины. Применение систематического кодав общем случае, хотя и позволяет упростить декодирование по сравнению с табличным способом, все же при значениях n порядка нескольких десятков не решает задачу практической реализации.
Совершенные и квазисовершенные коды
Совершенными (плотно упакованными) называют коды, в которых выполняются соотношения
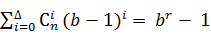 ,
,
где Δ — максимальная кратность исправляемых ошибок; b — основание кода; r — число проверочных символов. Они отличаются тем, что позволяют исправлять все ошибки кратностью D или меньше и ни одной ошибки кратности больше D.
Число известных совершенных кодов ограничено кодами Хэмминга значности
n = (br — 1)/(b — 1)
и бинарным циклическим кодом Голея.
Квазисовершенными принято называть коды, исправляющие все ошибки кратности D и
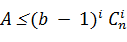
ошибок кратности D+1 при условии, что
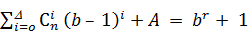 .
.
Класс квазисовершенных кодов значительно шире, чем класс плотно упакованных кодов. Совершенные и квазисовершенные коды обеспечивают максимум вероятности правильного приемакомбинации при равновероятных ошибках в канале связи.
Циклические коды
Был предложен ряд кодов и способов декодирования, при которых сложность декодера растет не экспоненциально, а лишь как некоторая степень n. В классе линейных систематических двоичных кодов это — циклические коды. Циклические коды просты в реализации и при невысокой избыточности обладают хорошими свойствами обнаружения ошибок.
Циклические кодыполучили очень широкое распространениекак в технике связи, так и в компьютерных средствах хранения информации. В зарубежных источниках циклические коды обычно называют избыточной циклической проверкой (CRC, Cyclic Redundancy Check).
Рассмотрим данный класс кодов подробнее. Название циклических кодов связано с тем, что каждая кодовая комбинация, получаемая путем циклической перестановки символов, также принадлежит коду. Так, например, циклические перестановки комбинации 1000101 будут также кодовыми комбинациями 0001011, 0010110, 0101100 и т.д.
Представление кодовых комбинаций в виде многочленов F(x) позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Сложение двоичных многочленов сводится к сложению по mod2 коэффициентов при равных степенях переменной x. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по mod2.
Деление осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложения по mod2. Циклическая перестановка кодовой комбинации эквивалентна умножению полинома F(x) на x с заменой на единицу переменной со степенью, превышающую степень полинома.
Любой полином G(x) степени r < n, который делит без остатка двучлен xn -1, может быть порождающим полиномом циклического (n, k)-кода, где
k = n - r. В этот код входят те полиномы, которые без остатка делятся на G(x).
Особую роль в теории циклических кодов играют неприводимые многочлены G(x), т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней.
Идея построения циклического кода (n, k) сводится к тому, что полином Q(x), представляющий информационную часть кодовой комбинации, нужно преобразовать в полином F(x) степени не более n - 1, который без остатка делится на порождающий полином G(x) (неприводимый многочлен) степени
r = n - k. Рассмотрим последовательность операций построения циклического кода:
- представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x);
- умножаем Q(x) на одночлен xr и получаем Q(x)xr;
- делим полином Q(x)xr на порождающий полином G(x) степени r, при этом получаем частное от деления C(x) такой же степени, что и Q(x)
Q(x)xr /G(x) = C(x) Å R(x)/G(x) ,
где R(x) – остаток от деления Q(x)xr на G(x);
- умножив обе части на G(x), получим
F(x) = C(x)G(x) = Q(x)xr Å R(x) .
Полином F(x) делится без остатка на G(x), т.е. представляет собой разрешенную комбинацию циклического (n,k)-кода.
Таким образом, разрешенную кодовую комбинацию циклического кода можно получить двумя способами: умножением кодовой комбинации простого кода C(x) на полином G(x) или умножением кодовой комбинации Q(x) простого кода на одночлен xr и добавлением к этому произведению остатка R(x).
В первом случае информационные и проверочные разряды не отделены друг от друга (код получается неразделимым). Во втором случае получается разделимый код. Этот код достаточно широко используется на практике, поскольку процесс декодирования и обнаружения ошибок при использовании разделимого кода выполняется проще.
Рассмотрим пример разделяемого циклического кода (9,5)с порождающим полиномом
G(x) = х4 + х + 1 (r = 4) .
В качестве информационной части кодовой комбинации возьмем полином
Q(x) = х4 + х2 + х + 1 .
Умножение Q(x) на xr эквивалентно повышению степени многочлена на r.
Q(x) = х4 + х2 + х + 1 ® 10111 .
Q(x)xr = (х4 + х2 + х + 1)х4 = х8 + х6 + х5 + х4 ® 101110000 .
Формирование проверочной группы осуществляется в процессе деления Q(x)xr на G(x).
| x2 |
| x3 |
| x4 |
| x |
| 1 |
| G(x) = x4 + x + 1 |
| 000011101 |
| 00101 |
Рис. 6.13. Структурная схема формирования проверочной группы
| К1 |
| Выход |
| Регистр задержки |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 4 |
| К2 |
Рис. 6.14. Упрощённая структурная схема кодера
Такая последовательность операций (суммирования) при делении Q(x)xr на G(x) может быть осуществлена с помощью r-ячеечного сдвигающего регистра с обратными связями между ячейками. Эти связи осуществляются через сумматоры по mod2. Делимое в виде кодовой группы, представляющей собой полином Q(x)xr , старшим разрядом подаётся на вход сдвигающего регистра, а полином G(x) вводится в регистр в виде структуры обратных связей через сумматоры. Место включения сумматоров определяется структурой полинома G(x) (рис. 6.13 и 6.14).
В результате деления получаем частное от деления C(x) = x4+x2®10100и остаток от деления R(x) = x3+x2®1100. Для получения разрешенной кодовой комбинации остаток (проверочная группа) помещается на место "пустых" разрядов Q(x)xr, т.е.
F(x)= x4+x2+x4+x2+x4+x2 ® 101111100 .
Данная комбинация отправляется в канал связи. Аналогичные операции выполняются для других информационных комбинаций.
Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок.
При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.
Однако обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью и будут рассмотрены ниже.
Прочие классы блочных коды
Наряду с циклическими кодами на практике используются и другие типы кодов, обладающие различными свойствами. Подробное рассмотрение всех классов кодов выходит за рамки настоящего курса, поэтому приведём только их краткую характеристику.
Например, среди циклических кодов особое значение имеет класс кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза-Чоудхури-Хоквингема (обозначаемые сокращением БЧХ) отличаются сравнительно просто реализуемой процедурой декодирования.
Относительно простой является процедура мажоритарного декодирования, применимая для некоторого класса двоичных линейных, в том числе циклических кодов. Основана она на том, что в этих кодах каждый информационный символ можно несколькими способами выразить через другие символы кодовой комбинации.
| Рис. 6.15. Структура блока итеративного кода |
| Информация |
| Проверка |
| Проверка |
| k1 |
| n1 - k1 |


 Мощные коды (т.е. коды с длинными блоками и большим кодовым расстоянием d) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код (рис. 6.15) из двух линейных систематических кодов (n1,k1) и (n2,k2). Минимальное кодовое расстояние для двумерного итеративного кода d=d1d2, где d1 и d2 — соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступеней.
Мощные коды (т.е. коды с длинными блоками и большим кодовым расстоянием d) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код (рис. 6.15) из двух линейных систематических кодов (n1,k1) и (n2,k2). Минимальное кодовое расстояние для двумерного итеративного кода d=d1d2, где d1 и d2 — соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступеней.
На итеративный кодпохож каскадный код, но между ними имеется существенное различие. Первая ступень кодирования в каскадном коде является линейным систематическим двоичным кодом (внутренний код), каждая комбинация которого рассматривается как один символ недвоичного кода второй ступени (внешнего).
При приёме сначала декодируются (с обнаружением или исправлением ошибок) все строки (блоки) внутреннего кода, а затем декодируется блок внешнего m-ичного кода, причем исправляются ошибки и стирания, оставшиеся после декодирования внутреннего кода (рис. 6.16).
| Канал |
| Рис. 6.16. Схема каскадного кодирования и декодирования |



 В качестве внешнего кода используют обычно m-ичный код Рида-Соломона, который является подклассом кодов БЧХ и обеспечивает наибольше возможное d при заданных n2 и k2, если n2<m. Каскадные коды во многих случаях наиболее перспективны среди известных блочных помехоустойчивых кодов.
В качестве внешнего кода используют обычно m-ичный код Рида-Соломона, который является подклассом кодов БЧХ и обеспечивает наибольше возможное d при заданных n2 и k2, если n2<m. Каскадные коды во многих случаях наиболее перспективны среди известных блочных помехоустойчивых кодов.
Метод перемежения
Для каналов с группированием ошибокчасто применяют метод перемежения символов, или декорреляции ошибок. Он заключается в том, что символы, входящие в одну кодовую комбинацию, передаются не непосредственно друг за другом, а перемежаются символами других кодовых комбинаций.
Если интервал между символами, входящими в одну комбинацию, сделать больше максимально возможной длины группы ошибок, то в пределах комбинации группирования ошибок не будет. Группа ошибок распределится в виде одиночных ошибок на группу комбинаций. Одиночные ошибки будут легко обнаружены (исправлены) декодером.
Свёрточные коды
Все рассмотренные до сих пор коды относятся к числу так называемых блочных кодов. В блочных кодах последовательность передаваемых символов разделена блоки по n символов в каждом. При этом обработка символов осуществляется по-блочно.
В настоящее время широкое распространение и применение получили непрерывные коды, в которых деление на блоки отсутствует. Непрерывное кодирование осуществляется последовательно по мере поступления кодируемых символов по некоторым рекуррентным соотношениям, поэтому такие коды называются рекуррентными.
Одной из разновидностей рекуррентных кодов, получившей наибольшую популярность в современных системах передачи информации, являются свёрточные коды (convolutional code). Свёрточные коды можно генерировать с помощью линейных регистров сдвига (рис. 6.17), выполняющих операцию свёртки информационной последовательности и импульсной характеристики регистров (порождающей последовательности).
В общем случае при кодировании в поток входящих информационных символов вставляются проверочные символы, при этом на каждые n кодовых символов приходится k информационных. Скорость такого кода R = k/n (k/n-свёрточный код). В рассмотренных примерах k = 1, n = 2, R = 1/2.
| Рис. 6.17,а. Структурная схема свёрточного систематического кодирования (1/2) |
| 1 |
| Выход |
| D |
| D |
| 2 |
| Вход |
| 00111110 |
| 0110 |
| Рис. 6.17,б. Структурная схема свёрточного несистематического кодирования (1/2) |
| D |
| D |
| Вход |
| 0110 |
| Выход |
| 00111010 |
| 1 |
| 2 |
Работу кодера удобно описывать при помощи диаграммы состояний, представляющей собой направленный граф, вершины которого отождествляются с возможными состояниями кодера, а рёбра, помеченные стрелками, указывают на возможные переходы между состояниями (рис. 6.18).
| Рис. 6.18. Диаграмма состояний ССК (1/2) |
| 10 |
| 01 |
| 11 |
| Вершины диаграммы |
| 00 |
| 00 |
| 01 |
| 10 |
| 11 |
| 01 |
| 00 |
| 10 |
| 11 |
Рассмотренную диаграмму состояний можно развернуть во времени, и при этом получим так называемую решётчатую диаграмму (рис. 6.19). На диаграмме переходы в другие или те же состояния кодера показаны в виде прерывистой линии, если на вход кодера поступила 1, и в виде сплошной линии, если на вход кодера поступил 0.
Начало диаграммы обозначает переходной режим кодера (из нулевого состояния), и уже через три такта структура диаграммы становится повторяющейся. В каждом узле диаграммы сходятся две ветви, являющиеся окончаниями двух путей на диаграмме, и из каждого узла исходит тоже две ветви. В общем случае ν-разрядного регистра с k0 информационными символами, приходящимися на один цикл опроса коммутатора, в любом из 2k0(ν - 1) узлов решётчатой диаграммы, соответствующих её сечению в какой-либо такт работы, сходится 2k0 ветвей, столько же ветвей исходит из любого узла.
Передаваемой информационной последовательности символов соответствует конкретная (взаимно-однозначная) последовательность состояний кодера, задающая определённый путь через совокупность узлов на решётчатой диаграмме.
| t |
Дата добавления: 2016-01-03; просмотров: 776;
