ГЕОМЕТРИЧЕСКАЯ И ЭНЕРГЕТИЧЕСКАЯ ИНТЕРПРЕТАЦИИ СЛАГАЕМЫХ, ВХОДЯЩИХ В УРАВНЕНИЕ БЕРНУЛЛИ

Обратимся к интерпретации отдельных слагаемых, входящих в урав­нение Бернулли для несжимаемой (капельной) жидкости (r = const). Го­ризонтальная координатная плоскость хОу, от которой отсчитывается ко­ордината z при решении гидравлических задач, называется плоскостью сравнения и обозначается на чертежах 0 - 0. Из вывода уравнения (7.2.11) следует, что z - это координата произвольной точки живого сечения w, а р - это гидродинамическое давле­ние в этой же точке. Из гидростати­ки известно, что отношение p/rg рав­но высоте столба жидкости, который создает давление, равное р.

Чтобы исключить возмущения потока, измерительные открытые трубки присоединяют к точкам жи­вого сечения, совпадающим с грани­цей потока (рис. 7.4).

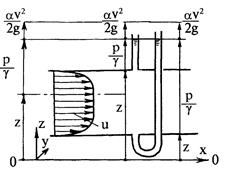Рис.7.4. Геометрическая интерпретация слагаемых, входящих в уравнение Бернулли

С учетом изложенного выше можно дать следующую геометричес­кую интерпретацию слагаемых, вхо­дящих в уравнение Бернулли:

z - превышение над плоскостью сравнения (геодезическая отметка) любой точки живого сечения потока;

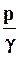- пьезометрическая высота в этой же точке, т.е. высота, на которую поднимается вода в открытой трубке, присоединенной к этой точке;

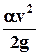- всегда положительна и имеет размерность длины;

в соответствии с уравнением (7.2.11) эту величину откладывают вверх от отметки .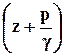

Кроме того, можно дать энергетическую интерпретацию слагаемых, входящих в уравнение Бернулли:

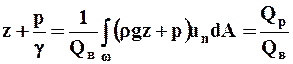- отношение потока потенциальной энергии (обусловленного течением жидкости) через живое сечение к ве­совому расходу;

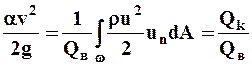- отношение потока кинетической энергии поступательного движения жидких частиц через сечение к весовому расходу;

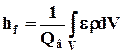- мощность (механическая энергия в единицу

времени), которая переходит в тепло внутри объема V, т.е. в трубопро­воде между сечениями 1 - 1 и 2 - 2, другими словами, диссипированная мощность, отнесенная к весовому расходу.