ДЕРЕВО СОБЫТИЙ - ДС (EVENT TREE ANALYSIS - ЕTA)

Дерево событий - алгоритм рассмотрения событий, исходящих от основного события (аварийной ситуации).

Дерево событий (ДС) используется для определения и анализа последовательности (вариантов) развития аварии, включающей сложные взаимодействия между техническими системами обеспечения безопасности. Вероятность каждого сценария развития аварийной ситуации рассчитывается путем умножения вероятности основного события на вероятность конечного события. При его построении используется прямая логика. Все значения P очень малы. Дерево не дает численных решений.

ПРИМЕР. Допустим, путем выполнения ПАО было выявлено, что критической частью реактора, т.е. подсистемой, с которой начинается риск, является система охлаждения реактора; таким образом, анализ начинается с просмотра последовательности возможных событий с момента разрушения трубопровода холодильной установки, называемого инициирующим событием, вероятность которого равна PA (рис. 6.9.1), т.е. авария начинается с разрушения (поломки) трубопровода - событие A. Далее анализируются возможные варианты развития событий (B, C, D и E), которые могут последовать за разрушением трубопровода. На рис. 6.9.1 изображено дерево исходных событий, отображающее все возможные альтернативы. На первой ветви рассматривается состояние электрического питания. Если питание есть, следующей подвергается анализу аварийная система охлаждения активной зоны реактора (АСОР). Отказ АСОР приводит к расплавлению топлива и к различным, в зависимости от целостности конструкции, утечкам радиоактивных продуктов.

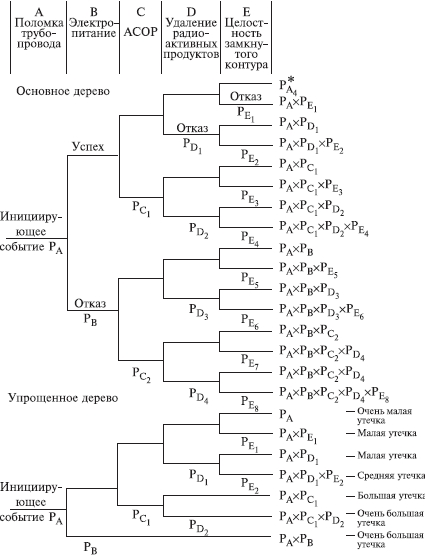
Рис. 6.9.1. Дерево событий

Для анализа с использованием двоичной системы, в которой элементы либо выполняют свои функции, либо отказывают, число потенциальных отказов равно 2N-1, где N - число рассматриваемых элементов. На практике исходное дерево можно упростить с помощью инженерной логики и свести к более простому дереву, изображенному в нижней части рис. 6.9.1. В первую очередь представляет интерес вопрос о наличии электрического питания. Вопрос заключается в том, какова вероятность PB отказа электропитания и какое действие этот отказ оказывает на другие системы защиты. Если нет электрического питания, фактически никакие действия, предусмотренные на случай аварии с использованием для охлаждения активной зоны реактора распылителей, не могут производиться. В результате упрощенное дерево событий не содержит выбора в случае отсутствия электрического питания, и может произойти большая утечка, вероятность которой равна PA(PB. В случае, если отказ в подаче электрической энергии зависит от поломки трубопровода системы охлаждения реактора, вероятность PB следует подсчитывать как условную вероятность для учета этой зависимости. Если электрическое питание имеется, следующие варианты при анализе зависят от состояния АСОР. Она может работать или не работать, и ее отказ с вероятностью PC1 ведет к последовательности событий, изображенной на рис. 6.9.1. Следует обратить внимание на то, что по-прежнему имеются различные варианты развития аварии. Если система удаления радиоактивных материалов работоспособна, радиоактивные утечки меньше, чем в случае ее отказа. Конечно, отказ в общем случае ведет к последовательности событий с меньшей вероятностью, чем в случае работоспособности. Рассмотрев все варианты дерева, можно получить спектр возможных утечек и соответствующие вероятности для различных последовательностей развития аварии (рис. 6.9.1). Верхняя линия дерева является основным вариантом аварии реактора. При данной последовательности предполагается, что трубопровод разрушается, а все системы обеспечения безопасности сохраняют работоспособность.

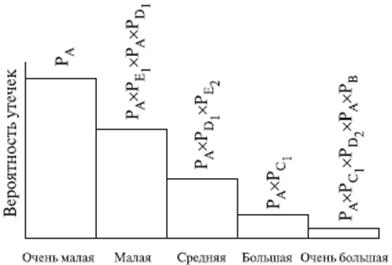
Рис. 6.9.1. Гистограмма вероятностей для различных величин утечек

ДЕРЕВО РЕШЕНИЙ

Дерево решений является разновидностью дерева событий. В дереве событий рабочие состояния системы не рассматриваются, так что сумма вероятностей всех событий не равна единице. В дереве решений все возможные состояния системы необходимо выразить через состояния элементов. Таким образом, все состояния системы взаимно увязаны, и их вероятность в сумме должна равняться единице. Деревья решений могут использоваться, если отказы всех элементов независимы или имеются элементы с несколькими возможными состояниями, а также есть односторонние зависимости. Они не могут использоваться при наличии двусторонних зависимостей и не обеспечивают логического анализа при выборе начальных событий.

ПРИМЕР. На рис. 6.10.1 показана система последовательно соединенных элементов, которая включает насос и клапан, имеющие соответственно вероятности безотказной работы 0,98 и 0,95, а также приведено дерево решений для этой системы. Следует отметить, что согласно принятому правилу верхняя ветвь соответствует желательному режиму работы системы, а нижняя - нежелательному. Дерево решений читается слева направо.

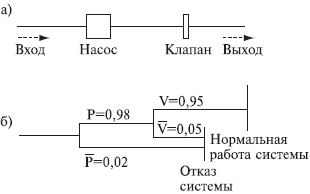
Рис. 6.10.1. Принципиальная схема (а) и дерево решений (б) для двухэлементной системы

Если насос не работает, система отказывает независимо от состояния клапана. Если насос работает, с помощью второй узловой точки изучается вопрос, работает ли клапан.

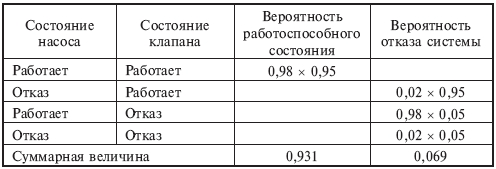
Вероятность безотказной работы системы: 0,98(0,95=0,931. Вероятность отказа: 0,98(0,05+0,02=0,069, а суммарная вероятность двух состояний системы равна единице.

Этот результат можно получить другим способом с помощью таблицы решения, которая для насоса и клапана имеет вид:

ЛОГИЧЕСКИЙ АНАЛИЗ

Логический анализ опасностей базируется на понятиях булевой алгебры (алгебры логики).

В алгебре логики переменные, обозначаемые заглавными буквами, имеют, как правило, смысл некоторых событий или факторов. Например, можно обозначить символом А событие, состоящие в повреждении какой-то части машины. Если это происходит, то мы говорим, что А=Т или что А истинно. Если это событие не происходит, говорим, что А=F или что А ложно. Такие высказывания справедливы для некоторого определенного интервала времени и вероятности, связанной с появлением события. Переменные в алгебре логики принимают два значения: истина или ложь (появление или непоявление). Аналогично и функции принимают два значения в зависимости от комбинации логических переменных. Функции образуются с помощью операций И, ИЛИ и НЕ. Смысл этих операций определяется таблицами истинности.

Истинное значение функции задается значениями переменных, входящих в нее. Например, пусть функция А имеет вид
А = ВС + D.

Чтобы определить истинное значение А, надо знать истинные значения четырех переменных. Вычисление значения отдельных членов ведется в порядке: (1) НЕ, (2) И и (3) ИЛИ. Таким образом, если В=ЛОЖЬ, С=ИСТИНА, D=ИСТИНА и Е=ЛОЖЬ, то, используя таблицы, получим:

А = FT + T = FT + TT = F + T = T.

Порядок вычисления операций может быть изменен применением скобок, причем выражения внутренних скобок вычисляются первыми. Например,

А = В() = F() = F() = F = FT = F.

При определенных навыках такие вычисления производятся достаточно быстро.

Особый интерес представляет применение алгебры логики для анализа предполагаемых производственных опасностей.

ПРИМЕР 1. На новой машине имеется цепной привод, который хоть и имеет защитное устройство, но в данном режиме работы должен быть убран. В нормальном режиме сама цепь работает с большим напряжением. Поэтому можно ожидать, что она быстро изнашивается и периодически рвется. Частицы от другого оборудования, попадая в цепь, также могут привести к ее обрыву. В случае обрыва цепи имеющееся защитное устройство, в зависимости от обстоятельств, может не обеспечить защиту рабочего.

Логическими переменными в этом случае будут:

А - защита цепи убрана;

В - цепь изнашивается и рвется;

С - технологические частицы приводят к обрыву цепи;

D - защита достаточна, чтобы защитить рабочего в любом случае.

Х - соответствует наличию опасной ситуации. Логическая операция примет вид

Х = А +B +C или Х = А + (В + С)

Для предотвращения опасной ситуации нужно, чтобы величина Х не стала истиной. Это имеет место, когда А ложно, D истинно или и В и С ложны одновременно.

Покажем еще пример использования принципов алгебры логики. В частности, применим отождествление истинного события с единицей, а ложного с нулем.

ПРИМЕР 2. При строительстве здания компрессорной станции проводились отделочные работы. Бригада отделочников, численностью пять человек, работала на лесах на высоте 3 м от нулевой отметки. При установке бадьи с раствором леса обрушились. Четыре человека были травмированы. Очевидцы несчастного случая, пострадавшие и должностные лица дали показания, на основании которых были выделены основные факторы несчастного случая.

Обозначим эти факторы логическими переменными (заглавными буквами):

А - леса удовлетворяли техническим условиям (ТУ) и правилам техники безопасности (ПТБ);

B - крановщик был нездоров;

C - нагрузка на леса удовлетворяла ТУ и ПТБ;

D - кран был неисправен;

E - на леса был установлен слишком тяжелый груз;

F - в момент опускания груза производился поворот стрелы;

G - перед началом работы крановщик осмотрел кран;

H - перед началом работы мастер осмотрел леса.

Анализ причин несчастного случая (отказа) при помощи булевых функций выполняют следующим образом. Установив факторы несчастного случая (НС) составляется матричная форма (табл. 6.11.1) для его описания. Если очевидец утверждает, что данный фактор имел место, в соответствующую графу заносят "1", если нет, то "0", при отсутствии адекватной информации делают прочерк "-". Затем составляют функцию алгебры логики (Fал). Для каждого очевидца определяют свою конъюнкцию. Если фактор имел место, то букву записывают в утвердительном значении; если нет - в виде инверсий; при "-" букву опускают. Полученную функцию минимизируют перебором всех эквивалентных формул (либо применяя соответствующие методы) и подвергают анализу, при котором устанавливают основные причины несчастного случая и сопутствующие им факторы.

Таблица 6.11.1