Analysis of the MP in the stages of monitoring, testing, packaging and storage
Mathematical actions with results of measurements
Mathematical actions with one result of measurement
Mathematical actions with the result of measurement submitting to the discrete law of distribution of probability. Mathematical actions with the result of measurement submitting to the continuous law of distribution of probability.
Mathematical actions with several results of measurements
Mathematical actions with the results of measurements submitting to discrete laws of distribution of probability.
Mathematical actions with the results of measurements submitting to continuous laws of distribution of probability.
Approximate calculations
Idea of approximate calculations. The amendment on discrepancy of calculations. Uncertainty of result of calculations at independent results of measurements and in the presence of statistical communication between them.
The decision of systems of the equations containing results of measurements
Cumulative and joint equations. The decision of system of the cumulative equations containing results of measurements. The decision of system of the joint equations containing results of measurements
Now at the solution of problems of calculation, the analysis, optimization and forecasting of chemical and technological processes it is widely used mathematical models. With the advent of the COMPUTER there was a possibility to receive mathematical descriptions of processes, using as basic data results of normal operation of technological process. Collecting an initial statistical material in a mode of normal operation on an industrial facility received the name of passive experiment. Also traditional method when a big series of experiences with serial change of each of variables is put belongs to passive experiment. Advantage of passive experiment is lack of expenses for experiences. However value of factors of the mathematical description decides on considerable mistakes. Processing of skilled data for receiving mathematical model is carried out by statistical methods which allow to take information maximum from available experimental data, to optimize procedure of processing and the experiment analysis.
Application of statistical methods of data processing is connected with large volume of calculations therefore it is necessary to use the COMPUTER.
1. Statistical models of processes on the basis of passive experiment
At identification and the description of znachimost between random variables according to passive experiment apply methods correlation regression analyses. Between random variables can exist, so-called, correlation communication at which with change of one size changes distribution another. For the characteristic of a form of communication when studying the correlation importance uses the regression equation.
a. Definition of factors of the equation of multiple regression
The equation of multiple regression received according to passive experiment, registers in the form of a linear polynom more often:
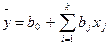 (1)
(1)
where b0 selective factor which is called as the free member of the equation; bj – the selective factors called by linear effects; xj – input measured and adjustable parameters of technological process (factors); 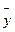 - an assessment of input measured parameter of process; k–number of factors.
- an assessment of input measured parameter of process; k–number of factors.
In real technological process always exists uncontrollable and uncontrollable parameters and change of size of target parameter U has casual character. Therefore when processing experimental data receive selective factors of b0 bj being estimates of theoretical factors β0 βj. The equation (1) is applied to creation of statistical models of a statics of processes of chemical technology. Such model does not bear necessary information on the process mechanism, its physical and chemical properties. However the equation of regression can be used for definition of optimum conditions of course of processes of optimum structures of preparation of mixes, etc.
Let passive experiment and the obtained data is made are reduced in table 1
Table 1.
| experience No. | Factors | Target parameter (parallel experiences) | ||||||
| Х1 | Х2 | У1 | У2 | ----- | Уu | ----- | Уm | |
| Х11 | Х21 | У11 | У21 | ----- | У1u | ----- | У1m | |
| Х12 | Х22 | У12 | У22 | ----- | У2u | ----- | У2m | |
| ----- | ----- | ----- | ---- | ----- | ------ | ----- | ----- | ----- |
| i | Х1i | Х2i | У1i | У2i | ----- | Уiu | ----- | Уim |
| ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- |
| N | X1N | X2N | U1N | U2N | ----- | UNU | ----- | UNM |
Here N – number of experiences, m-number of parallel experiences. It is required to define mathematical model in the form of a linear polynom for some process having input parameters х1, х2 and target parameter at:
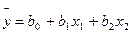 (2)
(2)
and to make the correlation regression analysis.
Let's provide the scheme of the correlation regression analysis on experimental data when each of N of experiences is repeated by m of times (таб.1).
On each iой to a line таб.1. let's find average value 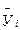 on m to parallel experiences:
on m to parallel experiences:
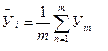 (3)
(3)
Then it is necessary to calculate value of target parameter on N to experiences;

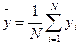 (4)
(4)
Let's calculate average value of factors 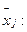
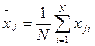 (5)
(5)
Let's find average quadratic deviations at and хj:
Sу = 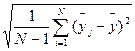 (6)
(6)
Sj = 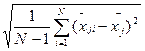 (7)
(7)
i, j = 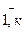
For simplification of calculations of factors of the equation of regression it is possible to normalize values at, x:
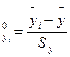 (8)
(8)
i=1, N
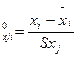 (9)
(9)
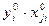 normirovanny values of target size and factors. Let's reduce results of a normirovka of all values in таб.2.
normirovanny values of target size and factors. Let's reduce results of a normirovka of all values in таб.2.
Table 2.
| experience No. | Factors | Target parameter (parallel experiences) | |
X 
| X 
| У0 | |
| --- i --- N | X 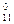 X
X 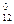 ---
X
---
X 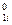 ---
X
---
X 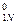
| X 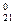 X
X 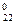 ---
X
---
X 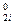 ---
X
---
X 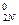
| at 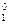 At
At 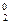 ---
At
---
At 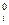 ---
At
---
At 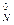
|
In new scale:
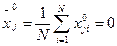
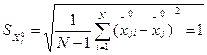
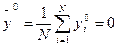
Sу = 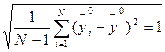
Let's calculate factors of correlation:
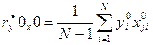
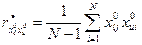 (11)
(11)
l, u=1,2 … k, l> u
The selective factors of correlation calculated on formulas (11) are equal to factors of correlation between the variables expressed in natural scale:
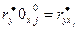 ;
; 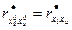 (12)
(12)
The mathematical statistics proves that the regression equation between normirovanny variables has no free member:
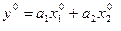 (13)
(13)
Ф (а1, а2) = 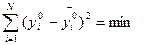 (14)
(14)
Or:
Ф (а1, а2) = 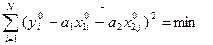 (15)
(15)
Necessary condition of a minimum of function F (а1, а2) is:
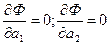 (16)
(16)
From (15) and (16) we have:
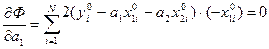
 (17)
(17)
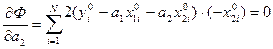
The system of the equations (17) can be copied in a look:
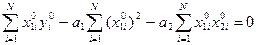 (18)
(18)
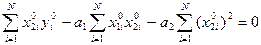
Let's pass to system of the normal equations:
а1 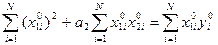 (19)
(19)
а1 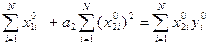
Let's increase the left and right parts of system (19) on 1 (/N-1):
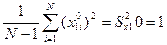 ;
; 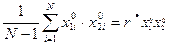 (20)
(20)
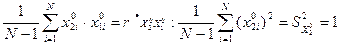 (21)
(21)
From (20), (21), (12) we will receive:
(22)
Having solved system of the equations (22) we will receive factors а1, а2. Value r 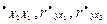 Let's calculate on formulas (11) using data таб.2.
Let's calculate on formulas (11) using data таб.2.
b. Factors of multiple correlation.
For definition of narrowness of communication of target parameter at and factors х1, х2 the factor of multiple correlation is calculated:
R= 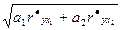 (23)
(23)
If factors 
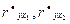 are according to sample of small volume, the size R, is calculated on a formula (23) and contains a big systematic mistake. Correlation of R it is feasible on a formula (24):
are according to sample of small volume, the size R, is calculated on a formula (23) and contains a big systematic mistake. Correlation of R it is feasible on a formula (24):
R1 = 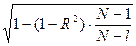 (24)
(24)
Where R1 - the corrected value factor of multiple correlation:
l–number of factors of the equation of regression.
The size of factor of R satisfies to an inequality:
0≤R≤1
R–it is an indicator of, as far as communication between random variables it is close to strict linear dependence. He equally notes also too big share of accident, and too big krivolineynost of this communication. If R considerably differs from unit, it is necessary to include additional factors in the equation of regression; again to calculate factors of the equation of regression and factors of multiple correlation. Nonlinearity of communication between studied variables can be the reason of small size R. In that case it is necessary to replace a linear polynom and to apply the corresponding method of processing of experiment.
Дата добавления: 2015-12-26; просмотров: 1077;
