Single measurement on the graduated scales

Sequence of performance of single measurement on the graduated scales of intervals and the relations. Options of use of aprioristic information. Amending.

The majority of technical measurements are straight lines single. Direct single measurements carry out in cases, if: there is no possibility of repeated measurements, at measurements there can be a destruction of object of measurement, economic feasibility takes place.

At direct single measurements use a unique value of counting of instrument readings. Being casual, single counting x includes tool, methodical and personal making errors of measurement, in each of which systematic and casual components can be allocated. Therefore before measurement the aprioristic assessment making errors with use of all available data should be defined. At definition of confidential borders of an error of result of measurements the confidential probability is accepted, as a rule, equal 0,95. The standard regulated the following form of record of result of direct single measurement of size

Repeated ravnotochny measurements

Need for repeated supervision of some physical size arises at existence in the course of measurements of considerable casual errors.

The technique of statistical processing of results of supervision consists of the following operations:

1. Carry out supervision and fix results of supervision of the same value of physical size:;

2. Exclude known systematic errors;

3. Find average arithmetic value of the corrected results of supervision:

4. Calculate an assessment of an average quadratic deviation of results of supervision:

5. Calculate an assessment of an average quadratic deviation of result of measurement:

6. Calculate confidential borders of a casual component of an error of measurements which without a sign is determined by a formula:

where – factor Styyudenta.

For symmetric confidential borders of an error the result of measurement of size is represented in shape:

Control questions

1. In what cases carry out repeated measurements?

2. List algorithms of processing of results of repeated supervision. 3. What criteria use for detection of rough errors?

Repeated measurement on an order scale. Bases of the theory of selective statistical control.

Repeated measurement on the graduated scales. Repeated measurement with ravnotochny values of counting. Repeated measurement with neravnotochny values of counting. Processing of several series of measurements.

Repeated measurement with ravnotochny values of counting

Fundamental idea of repeated measurement. Sequence of performance of repeated measurement on the graduated scales of intervals and the relations. Formation of the massif of experimental data. Amending. Exception of mistakes. Promotion and check of hypotheses about the law of distribution of probability of result of measurement. The solution of a return task at various laws of distribution of probability of result of measurement. Ensuring demanded accuracy of measurements.

Repeated measurement with neravnotochny values of counting

Average weighed. Dispersion of an average weighed. Solution of a return task.

Processing of results of several series of measurements

Homogeneous and non-uniform series of measurements. Check of a normality of results of measurements in each series. Check of the importance of distinction between average arithmetic values of result of measurement in two series. Check of a ravnorasseyannost of results of measurements in two series. Processing of results of homogeneous and non-uniform series of measurements.

Repeated ravnotochny measurements

Need for repeated supervision of some physical size arises at existence in the course of measurements of considerable casual errors.

Direct repeated measurements share on ravnotochny and neravnotochny measurements. Measurements which are led by gages of identical accuracy by the same technique under invariable external conditions are called as Ravnotochnymi. At ravnotochny measurements of SKO of results of all ranks of measurements are equal among themselves.

The problem of processing of results of measurements consists in finding of an assessment of the measured size and a confidential interval in which there is its true value. Processing should be carried out according to GOST 8.207-76 «GSI. Direct measurements with repeated supervision. Methods of processing of results of supervision. General provisions».

Initial information is a row from n (n> 4) results of measurements

X1, the X-th 2, x1 x2 from which known systematic errors - sample are excluded. The number of "n" depends on requirements to accuracy of received result and from real possibility to carry out repeated measurements.

The sequence of processing of results of direct repeated measurements consists of a number of stages:

I stage: Definition of dot estimates of the law of distribution of results of measurements.

Are defined:

- average arithmetic value x of the measured size;

- SKO of result of measurement of Sx;

- SKO of average arithmetic value S.

According to criteria misses are excluded, then repeated calculation of estimates of average arithmetic and its SKO is carried out. For more reliable calculation can other dot estimates will be defined: factor of an assimetriya of v, эксцесc ε and its counterexcess To;

П stage: Definition of the law of distribution of results of measurements or casual errors of measurements.

From sample of results of measurements х1.х2 хз..., x„ pass to sample of deviations from average arithmetic Akh1, Akh2, Akh3.... Akhp where Ah, = x, - x.

At identification of the law of distribution determine construction by the corrected results of measurements х1, where by i=I, 2..., n, a variation row (the ordered sample), and also Vi where y1=min (x1 and yn=max (In a variation row results of measurements or their deviation have x1 in ascending order; a row break into optimum number of t of identical intervals of grouping in length of h = (y1 + unitary enterprise)/t. Leah of practical application it is expedient to use mmin expression = 0,55п04 and ттах = 1,25п ° received for often meeting distributions with an excess in limits from 1,8 to 6, those from uniform Laplas before distribution. Required value of t in an interval ттin and ттах should be odd as at even value of t the middle of a curve of distribution it is artificial уплощается.

Define intervals of grouping of experimental data in a look
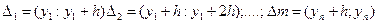also count up number of hits of n, (frequency) of results of measurements in each interval of grouping. The sum of these numbers should equal to number of measurements. On the received values count probabilities of hit of results of measurement to frequency in each of grouping intervals on a formula:

рk ₌ n) / п, where к=1,2 … t.

These calculations allow to construct the histogram, the range and a cumulative curve.

Drawing 7.1 - the Histogram, the range (and) and a cumulative curve

For creation of the histogram on an axis of results of supervision x ∆t intervals in ascending order numbers are postponed and on each interval is under construction in p1 rectangle in height. The area concluded under the schedule, is proportional to number of supervision of "n" Sometimes height of a rectangle postpone equal empirical density of probability р1 = pt/∆k = n k/(∆n k) which is an assessment of average density of n “n” interval In this case the area under the histogram is equal 1. At increase in number of intervals and respectively reduction of their length the histogram more and more comes nearer to a smooth curve - to graphics of density of distribution of probability.

The range represents the broken curve connecting the middle of the top bases of each column of the histogram; it reflects a form of a curve of distribution. Outside of the histogram on the right and at the left there are empty intervals in which the points corresponding to their middle, lie on an axis of abscissae. These points at creation of the range connect among themselves pieces; as a result together with an axis x the closed figure, which area according to rationing rules is formed, should be equal to 1 (unit) (or to number of supervision when using by frequency).

The cumulative curve is a schedule of statistical function of distribution. For its construction on an axis of results of supervision x postpone intervals Д4 in ascending order numbers and on each interval build a rectangle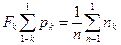

Fk value is called as a cumulative particular, and n sum - cumulative frequency. By the form constructed dependences the law of distribution of results of measurements can be estimated.

III stage: An assessment of the law of distribution by statistical criteria.
At number of supervision of n> 50 for identification of the law of distribution Pearson is used criteria!' - х2 (хи - a square) or Mizesa-Smirnov's criterion (ω2). At 50> п> 15 the compound criterion is applied to check of a normality of the law of distribution (by d - criterion), given in Gost8.207-76. At п <the 15th belonging of experimental distribution to the normal is not checked.

IV stage: Definition of confidential borders of a casual error.

If it was possible to define the law of distribution of results of measurements, with its use find a kvantilny multiplier of Zp at a preset value of confidential probability of R; in this case confidential borders of a casual error д = ± z p Sk

V stage: Delimitation of not excluded systematic error in results of measurements.

Borders of not excluded systematic error are accepted equal to limits of allowed main and additional errors of measuring instruments if their casual components are negligible. The confidential probability at delimitation 0 is accepted the equal confidential probability used at finding of borders of a casual error.

Metrological Supervision and state testing of measuring instruments. Metrological control the measurements, condition and use of measuring instruments. Organization, procedure and methods of verification of measuring instruments. The concept of verification, calibration, adjustment and calibration of measuring instruments. Calibration scheme. Public acceptance and routine tests measuring tools