Абстрактное бинарное дерево

Лекция Деревья

Деревья(trees) используются для представления отношения. Все деревья являются иерархическимипо своей сути. Интуитивное значение этого термина состоит в том, что между узлами дерева существует отношение "родительский-дочерний". Если ребро со­единяет узел n и узел т, причем узел п находится выше узла т, то узел n счи­тается родителем (parent) узла т, а узел т — его дочерним узлом(child) . В де­реве, изображенном на рис. 10.1,узлы В и С являются дочерними по отношению к узлу А. Дочерние узлы, имеющие одного и того же родителя, — например, уз­лы В и С — называются братьями(siblings) . Каждый узел дерева имеет по крайней мере одного родителя, причем в дереве существует только один узел, не имеющий предков. Такой узел называется корнем дерева(root) . На рис. 10.1корнем является узел А. Узел, у которого нет дочерних узлов, называется лис­том дерева(leaf). Листьями дерева, изображенного на рис. 10.1, являются узлы С, D, Е и F.

D E F

Рис. 10.1. Дерево общего в

Отношения между родительским и дочерним узлом с абстрактной точки зре­ния является отношением между предком(ancestor) и потомком(descendant). На рис. 10.1узел А является предком узла Д следовательно, узел D является по­томком узла А. Не все узлы могут быть связаны отношениями "предок-потомок": узлы В и С, например, не связаны родственными отношениями. Однако корень любого дерева является предком каждого его узла. Поддеревом(subtree) называется любой узел дерева со всеми его потомками. Поддеревом узлап является поддерево, корнем которого является узел n. Например, на рис. 10.2 показано поддерево дерева, изображенного на рис. 10.1. Корнем этого поддерева является узел В, а само поддерево является поддеревом узла А.

С формальной точки зрения, дерево общего вида(general tree) T представляет собой множество, состоящее из одного или нескольких узлов, принадлежащих непересекающимся подмножествам, указанным ниже.

• Отдельный узел r, корень.

• Множество поддеревьев корня r.

Бинарное дерево(binary tree) — это множество узлов Т, таких что

• множество Т пусто, или

• множество Т распадается на три непересекающихся подмножества:

• отдельный корень r, корень;

• два возможно пустых поддерева бинарного дерева, которые называются левым и правым поддеревьями(leaf and right subtrees) корня r, соответственно.

В качестве иллюстрации использования бинарных деревьев для представле­ния данных в иерархическом виде рассмотрим рис. 10.4. На этом рисунке би­нарные деревья представляют алгебраические выражения, содержащие бинарные операторы +, -, * и /. Для представления выражения а-b оператор помещается в корневой узел, а операнды а и b— в его левый и правый дочерние узлы, соответственно (рис. 10.4). На рис. 10.4, б представлено выражение a-b/с, где поддерево представляет подвыражение b/с. Аналогичная ситуация показана на рис. 10.4, в, где изображено выражение (а-b)*с. В узлах этих деревьев хранятся операнды выражений, а в остальных узлах — операторы. Скобки в этих деревьях не представлены. Бинарное дерево создает иерархию операций, т.е. дерево однозначно определяет порядок вычисления выражения.

б) в)

Рис. 10.4. Бинарные деревья, представляющие алгебраические выражения

Бинарное дерево поиска— это бинарное дерево, некоторым образом упорядоченное в соответ­ствии со значениями, содержащимися в его узлах. Каждый узел п бинарного де­рева поиска обладает следующими тремя свойствами:

• Значение узла п больше всех значений, содержащихся в левом поддереве TL.

• Значение узла п меньше всех значений, содержащихся в правом поддереве ТR.

• Деревья TL и ТR являются деревьями бинарного поиска.

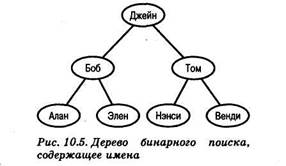
На рис. 10.5 показан пример бинарного дерева поиска. Как следует из его назва­ния, это дерево обеспечивает возможности поиска конкретного элемента. Позд­нее мы рассмотрим эту структуру данных более подробно.

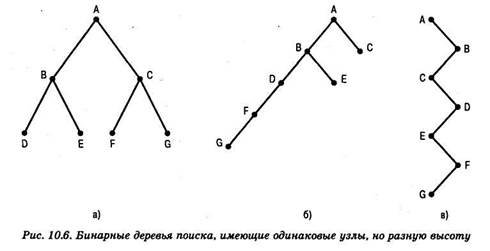
Высота деревьев. Деревья могут иметь разную форму. Например, хотя деревья, изображенные на рис. 10.6, состоят из одинаковых узлов, они имеют совершенно разную структуру. Каждое из этих деревьев содержит семь узлов, но некоторые деревья "выше" других. Высота (height) дерева — это количество узлов, располо­женных на самом длинном пути от корня к листу. Например, высота деревьев, по­казанных на рис. 10.6, равна 3, 5 и 7, соответственно. Интуитивное представление о высоте деревьев может привести к заключению, что их высота равна 2, 4 и 6, соответственно. Действительно, многие авторы используют именно интуитивное оп­ределение высоты дерева (подсчитывая количество ребер на самом длинном пути от корня до дерева. — Прим. ред.). Однако принятое нами определение позволяет более четко формулировать многие алгоритмы и свойства деревьев.

Полное, совершенное и сбалансированное дерево.В полном бинарном дереве(full binary tree), имеющем высоту h, все узлы, расположенные на уровнях, меньших уровня h, имеют по два дочерних узла. На рис. 10.7 представлено пол­ное бинарное дерево, имеющее высоту, равную 3. Каждый узел полного бинарно­го дерева имеет левое и правое поддерево, имеющие одинаковую высоту. Среди всех бинарных деревьев, высота которых равна h, полное бинарное дерево имеет максимально возможное количество листьев, и все они расположены на уровне h. Проще говоря, в полном бинарном дереве нет пропущенных узлов.

Доказывая свойства полных бинарных деревьев, подсчитывая количество их узлов, удобно пользоваться рекурсивным определением.

• Если дерево Т пусто, то оно является полным бинарным деревом, имеющим

высоту, равную 0.

• Если дерево T не пусто, и его высота равна h > 0, то дерево T является полным бинарным деревом, если поддеревья его корня являются полными бинарными деревьями, имеющими высоту h-1.

Это определение хорошо отражает рекурсивную природу бинарного дерева.

Совершенное бинарное дерево(complete binary tree), имеющее высоту h, — это бинарное дерево, которое является полным вплоть до уровня h-1, а уровень h заполнен слева направо так, как показано на рис. 10.8.

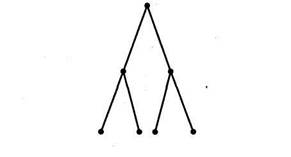
Рис. 10.8. Совершенное бинарное дерево

Очевидно, что полное бинарное дерево является совершенным.

Бинарное дерево называется сбалансированным по высоте(height balanced), или просто сбалансированным(balanced), если высота правого поддерева любого его узла отличается от высоты левого поддерева не больше, чем на 1. Бинарные деревья, изображенные на рис. 10.8и 10.6, а, яв­ляются сбалансированными, а деревья, представленные на рис. 10.6, б и 10.6, в — нет. Совершенное бинарное дерево является сбалансированным. Итак, повторим кратко введенные понятия.

Абстрактное бинарное дерево

B бинарном дереве существует несколько способов обхода. Стандартными являются три порядка обхода дерева: прямой, симметричный и обратный. Все они описываются в следующем разделе. Над абстрактным бинарным деревом выполняются следующие операции.