Способы представления бинарного дерева

Для представления бинарного дерева в языке C++ есть три возможности. Две из них основаны на использовании массивов, но обычно для реализации бинарного дерева используются указатели. В любом случае выбранная структура данных содержится как закрытая переменная-член в классе бинарных деревьев.

1. Представление бинарного дерева в виде массива.

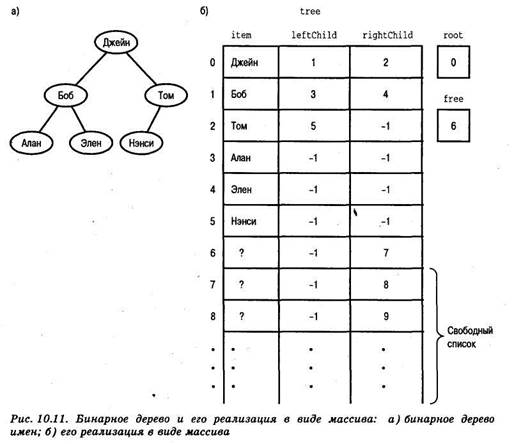
Переменная root является индексом корня дерева в массиве tree. Если де­рево пусто, значение переменной root равно -1. Переменные leftChild и rightChild в классе TreeNode являются индексами дочерних узлов. Если у данного узла нет левого дочернего узла, значение переменной leftChild равно -1. Если узел не имеет правого дочернего узла, значение переменной rightChild также равно -1.

На рис. 10.11показано би­нарное дерево и его реализация в виде массива.

При реализации дерева необхо­димо создать список доступных узлов, называемый свободным списком(free list).

2. Реализация совершенного дерева в виде массива.Предыдущая реализация ориентировалась на произвольное бинарное дерево, хотя дерево, изображенное на рис. 10.11,является совершенным. Если заранее известно, что бинарное дерево является совершенным, можно использовать более простую и экономную реали­зацию, основанную на массивах. Как указывалось ранее, совершенное дерево, имеющее высоту h, является полным вплоть до уровня h-1, а на уровне h запол­няется слева направо.

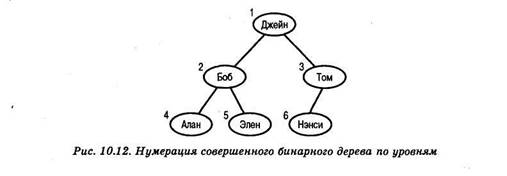
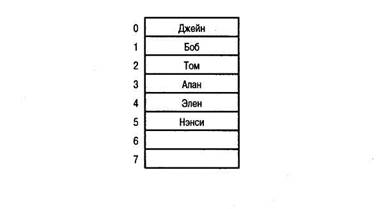
На рис. 10.12 показано совершенное бинарное дерево, изображенное ранее на рис. 10.11,а. Теперь его узлы пронумерованы по уровням. Корень имеет номер 0, его дочерние узлы (лежащие на следующем уровне) — 1 и 2. Узлы, принад­лежащие следующему уровню, нумеруются слева направо, т.е. их номера равны 3, 4 и 5, соответственно. Эти узлы записываются в массив tree в ячейки, соот­ветствующие их номерам. Иными словами, ячейка tree [i] содержит число i, как показано на рис. 10.13. Теперь по номеру tree [i] можно легко определить его дочерние и родительский узлы: индекс левого дочернего узла (если он суще­ствует) хранится в ячейке tree [2*i+1], индекс правого дочернего узла (если он существует) — в ячейке tree [2*i+2], а индекс родительского узла (если узел tree[i] не является корнем дерева) — в ячейке tree[(i-1)/2)].

Рис. 10.13. Реализация совершенного бинарного дерева, изобра­женного на рис. 10.12, в виде массива

Необходимо, чтобы при любых изменениях дере­во оставалось совершенным.

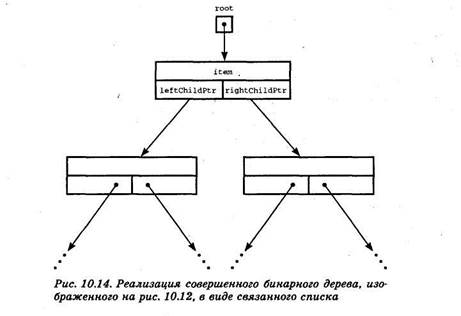
3. Представление бинарного дерева в виде связанного списка.Для связывания узлов дерева можно применить указатели, предусмотренные в языке С++.